Cây AVL trong cấu trúc dữ liệu và giải thuật

Nội dung chính

Cây AVL là gì?

Điều gì xảy ra nếu dữ liệu nhập vào cây tìm kiếm nhị phân (BST) là ở dạng đã được sắp thứ tự (tăng dần hoặc giảm dần). Nó sẽ trông giống như sau:

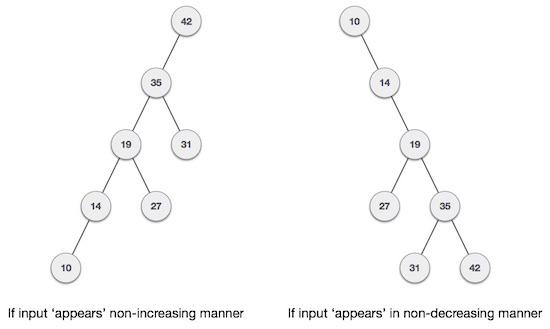
Nói chung, hiệu suất trường hợp xấu nhất của cây tìm kiếm nhị phân (BST) gần với các giải thuật tìm kiếm tuyến tính, tức là Ο(n). Với dữ liệu thời gian thực, chúng ta không thể dự đoán mẫu dữ liệu và các tần số của nó. Vì thế, điều cần thiết phát sinh ở đây là để cân bằng cây tìm kiếm nhị phân đang tồn tại.

Cây AVL (viết tắt của tên các nhà phát minh Adelson, Velski và Landis) là cây tìm kiếm nhị phân có độ cân bằng cao. Cây AVL kiểm tra độ cao của các cây con bên trái và cây con bên phải và bảo đảm rằng hiệu số giữa chúng là không lớn hơn 1. Hiệu số này được gọi là Balance Factor (Nhân tố cân bằng).

Dưới đây là hình ví dụ minh họa ba cây, trong đó cây đầu tiên là cân bằng, cây thứ hai và thứ ba là không cân bằng.

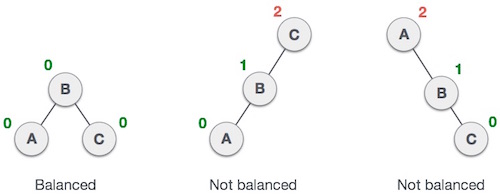
Trong cây thứ hai, cây con bên trái của C có độ cao là 2 và cây con bên phải có độ cao là 0, do đó hiệu số là 2. Trong cây thứ ba, cây con bên phải của A có độ cao là 2 và cây con bên trái có độ cao là 0, do đó hiệu số cũng là 2. Trong khi cây AVL chỉ chấp nhận hiệu số (hay Nhân tố cân bằng) là 1.

BalanceFactor = height(left-sutree) − height(right-sutree)

Nếu hiệu số giữa độ cao của các cây con bên trái và cây con bên phải là lớn hơn 1 thì cây được cân bằng bởi sử dụng một số kỹ thuật quay AVL được trình bày dưới đây.

Kỹ thuật quay cây AVL

Để làm cho cây tự cân bằng, một cây AVL có thể thực hiện 4 loại kỹ thuật quay sau:

Kỹ thuật quay trái

Kỹ thuật quay phải

Kỹ thuật quay trái-phải

Kỹ thuật quay phải-trái

Hai kỹ thuật quay đầu tiên là các kỹ thuật quay đơn và hai kỹ thuật quay còn lại là các kỹ thuật quay ghép.

Phần tiếp theo chúng ta sẽ tìm hiểu chi tiết từng kỹ thuật quay với hình minh họa đơn giản và dễ hiểu.

Kỹ thuật quay trái cây AVL

Nếu một cây trở nên không cân bằng khi một nút được chèn vào trong cây con bên phải của cây con bên phải thì chúng ta có thể thực hiện kỹ thuật quay trái đơn như sau:

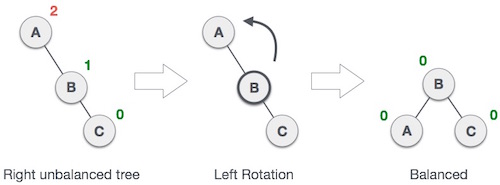
Trong hình minh họa trên, nút A trở nên không cân bằng khi một nút (nút C) được chèn vào cây con bên phải của cây con bên phải của nút A. Chúng ta thực hiện kỹ thuật quay trái để làm A trở thành cây con bên trái của B.

Kỹ thuật quay phải cây AVL

Cây AVL trở nên không cân bằng nếu một nút được chèn vào cây con bên trái của cây con bên trái. Để cây cân bằng, chúng ta thực hiện kỹ thuật quay phải như sau:

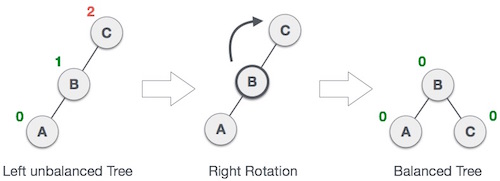
Như hình minh họa, nút không cân bằng sẽ trở thành cây con bên phải của cây con bên trái của nó bằng kỹ thuật quay phải.

Kỹ thuật quay trái-phải cây AVL

Kỹ thuật quay ghép là khá phức tạp so với hai kỹ thuật quay đơn vừa giới thiệu trên. Để hiểu kỹ thuật quay này nhanh hơn, bạn cần phải ghi chú từng hành động được thực hiện trong khi quay. Một kỹ thuật quay trái-phải là sự kết hợp của kỹ thuật quay trái được theo sau bởi kỹ thuật quay phải.