Tính thể tích hình chóp như thế nào? Bài viết dưới đây sẽ giới thiệu cho bạn về công thức và cách tính thể tích hình chóp, khối chóp đều, mời các bạn tham khảo.
Hình chóp là gì?
Hình chóp là hình có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này được gọi là đỉnh của hình chóp.
Đường cao của hình chóp là đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy.
Tên gọi của hình chóp dựa vào đa giác đáy: hình chóp tam giác có đáy là tam giác, hình chóp tứ giác có đáy là tứ giác.
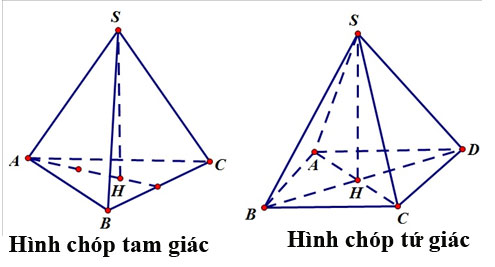
Các khối chóp đặc biệt
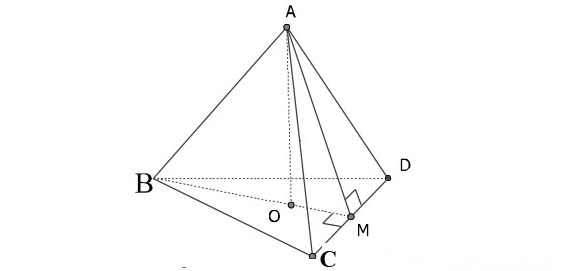
Hình chóp tứ diện đều
Hình chóp tứ diện đều là hình chóp có tất cả các cạnh bằng nhau, tất cả các mặt đều là các tam giác đều. Trong đó, O là trọng tâm của tam giác đáy và AO vuông góc với (BCD).
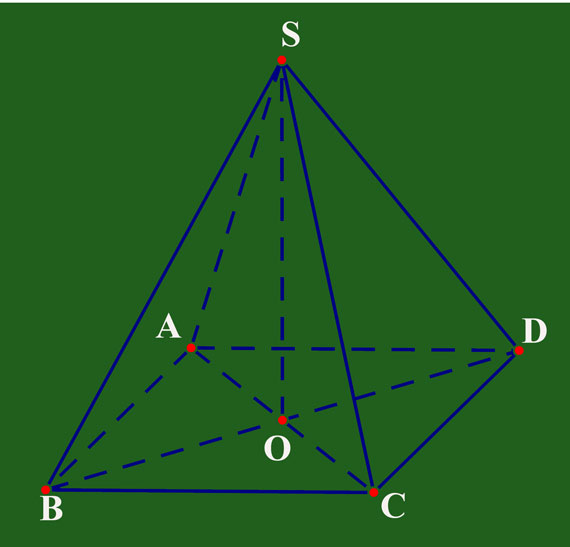
Hình chóp tứ giác đều
Hình chóp tứ giác đều là hình chóp có tất cả các cạnh bên bằng nhau, đa giác đáy là hình vuông tâm O, SO vuông góc với mặt đáy (ABCD).
Công thức tính chu vi hình chóp
Chu vi hình chóp bằng tổng chu vi mặt đáy và các mặt bên (áp dụng cho hình chóp tam giác, hình chóp tứ giác).
Công thức:
P = Pđáy + Pcác mặt bên
Trong đó:
Pđáy là chu vi mặt đáy
Pcác mặt bên là chu vi các mặt bên
Thể tích hình chóp
(Áp dụng cho hình chóp tam giác, hình chóp tứ giác)
Công thức
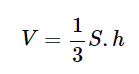
Trong đó:
S là diện tích đáyh là chiều cao
Bài tập về tính thể tích khối chóp
Bài 1:
Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a, cạnh bên SA vuông góc với mặt phẳng đáy và SC tạo với mặt đáy một góc bằng 60º. Tính thể tích khối chóp S.ABCD.
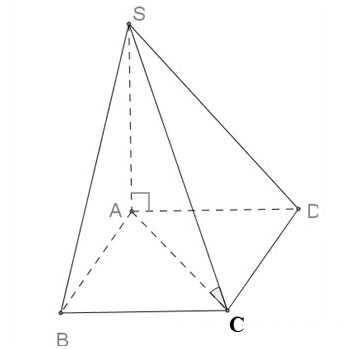
Giải:

Bài 2: Cho hình chóp tứ giác đều SABCD có các mặt bên là những tam giác đều, AB=8m, O là trung điểm của AC. Hình chóp SABCD có mấy cạnh? Độ dài SO là bao nhiêu?
Giải:
Hình chóp SABCD là hình chóp tứ giác nên có 8 cạnh.
Hình chóp SABCD đều nên đáy ABCD là hình vuông và tam giác OAB vuông cân tại O.
Áp dụng định lí Py-ta-go vào tam giác vuông OAB có
AB² = OB²+ OB²→ AB² = 2OA²
OA=
Hình chóp có các mặt bên là tam giác đều nên tam giác SAB là tam giác đều. Do đó:
SA = AB = 8m
Ta có SO vuông góc với OA nên tam giác SOA vuông tại O. Áp dụng định lí Py-ta-go ta có:
SB² = OS² + OA²





