Bạn cần phải ôn tập cho kỳ thi sắp tới nhưng bây giờ bạn vẫn chưa biết gì về hình cầu? Cũng như không biết công thức và cách tính diện tích, thể tích hình cầu ra sao? Đừng lo, hàng ngũ Trường THPT Phạm Hồng Thái chúng tôi sẽ hướng dẫn bạn cách tính diện tích và thể tích hình cầu vô cùng đơn thuần, chi tiết, dễ hiểu thông qua bài viết sau.
Mục lục bài viết [Ẩn]

khái niệm hình cầu là gì? Mặt cầu là gì?
Theo khái niệm toán học, trong không gian ba chiều, khi quay nửa hình tròn (O, R) 1 vòng quanh đường kính AB cố định thì được 1 hình cầu.
- Nửa đường tròn trong phép quay trên là 1 mặt cầu.
- Điểm O là tâm hình cầu và R là bán kính của hình cầu hay mặt cầu đó.

Mặt cầu là tập hợp những điểm nằm cách đều điểm O (tâm hình cầu) 1 khoảng cố định cho trước không đổi = R (bán kính) tức R= OA.

* Tính chất của hình cầu
- Trục đối xứng của hình cầu là bất kỳ đường thẳng nào giao nhau với hình cầu và đi qua tâm của nó. lúc đó, xoay 1 quả cầu xung quanh trục này ở bất kỳ góc độ nào cũng sẽ biến nó thành chính nó.
- Mặt phẳng phản xạ là một mặt phẳng cắt hình được đề cập qua tâm của nó chia hình cầu thành hai phần bằng nhau.
Công thức tính diện tích mặt cầu, thể tích hình cầu
1. Công thức tính diện tích mặt cầu
Theo khái niệm, diện tích mặt cầu được tính bằng 4 lần diện tích hình tròn lớn, hay bằng bốn lần hằng số Pi nhân với bình phương bán kính của hình cầu.


Trong đó:
- S là diện tích mặt cầu
- r là bán kính mặt cầu/hình cầu
- d là đường kính mặt cầu/hình cầu
- π là 3.14
2. Công thức tính diện tích xung quanh hình cầu
Để tính diện tích xung quanh hình cầu, chúng ta có thể sử dụng công thức sau:
Sxq = 4πr^2
Trong đó:
- Sxq là diện tích xung quanh hình cầu
- π (pi) là một hằng số xấp xỉ 3.14159
- r là bán kính của hình cầu
Với công thức này, chúng ta nhân bán kính của hình cầu với 2, sau đó nhân kết quả với π để tính diện tích xung quanh hình cầu.
3. Công thức tính thể tích hình cầu (khối cầu)
Theo khái niệm, thể tích hình cầu (hay thể tích khối cầu) được tính bằng ba phần tư của Pi nhân với lập phương bán kính hình cầu.
tương tự, để tính thể tích khối cầu, chỉ cần tìm bán kính hình cầu (hoặc đường kính). Sau đó thay vận dụng vào công thức V = ⁴⁄₃πr³ để tính.

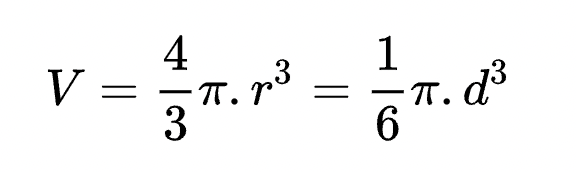
- V là thể tích khối cầu (đơn vị m3)
- π là số pi, có trị giá sấp sỉ 3,14
- r là bán kính khối cầu
- d là bán kính mặt cầu/hình cầu
Lưu ý: Đơn vị của thể tích là đơn vị khối (cm3, m3,…)

Hướng dẫn cách tính thể tích hình cầu
Bước 1: Viết công thức tính hình cầu ra giấy
trước hết, bạn viết ra giấy công thức tính thể tích hình cầu: V = ⁴⁄₃π.r³.

Bước 2: Đọc đề tìm bán kính
Sau đó, độc giả đề nếu như đề cho sẳn bán kính thì bạn ghi ra giấy. Nhưng nếu như đề cho bạn đường kính thì bạn có thể vận dụng công thức V = 1⁄6π.d³.
Hoặc bạn cũng có thể lấy đường kính chia 2 để ra bán kính rồi vận dụng công thức như bước 1.

Giả sử trường hợp khó hơn, đề chỉ cho bạn diện dích mặt cầu (S). Bạn có thể tìm bán kính bằng cách lấy diện tích mặt cầu chia cho 4π, sau đó tính căn bậc hai của kết quả này là ra. tức là:
r = √(S/4π) (“bán kính bằng căn bậc hai của thương số diện tích và 4π”).
Bước 3: Tiến hành tính luỹ thừa bậc 3 của bán kính
Tới đây, bạn chỉ cần tính luỹ thừa bậc 3 của bán kính bằng cách đem bán kính nhân ba lần với chính nó hoặc nâng nó lên số mũ ba
Ví dụ: (1 cm)3 = 1 cm x 1 cm x 1 cm = 1
(2 cm)3 = 2 cm x 2 cm x 2 cm = 8

Bước 4: Tiếp tục nhân luỹ thừa bậc 3 của bán kính với 4/3
Tiếp tới, bạn bạn thay trị giá r³ vừa tính được vào công thức V = ⁴⁄₃πr³ để phương trình gọn hơn. Ví dụ đường tròn có bán kính là 1cm:
- 4/3 x 1 = 4/3
- V = ⁴⁄₃ x π x 1, hay V = ⁴⁄₃π.

Bước 5: Nhân biểu thức vừa tính được với π (số pi)
Cuối cùng, bạn đặt π vào phép tính và nhân trị giá của nó với 4/3. Trong đó, trị giá của π tương đương với 3.14159. nếu như không bạn cũng có thể để nguyên π trong đáp án theo dạng V = ⁴⁄₃π là xong.
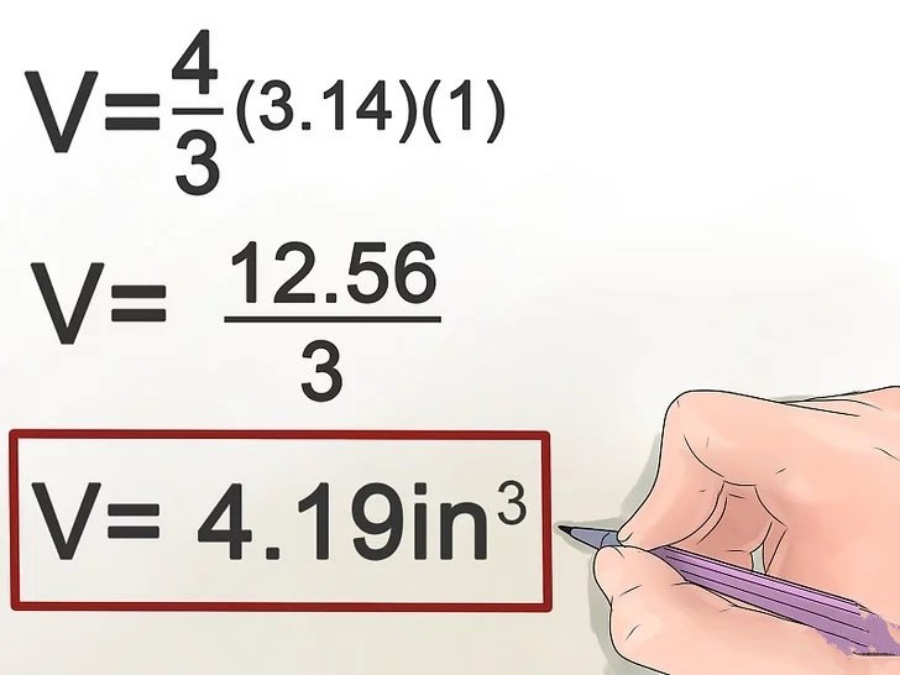
Ví dụ: V = 3.14159 x 4/3 = 4.1887.
Kết luận thể tích của hình cầu với bán kính bằng 1 là 4.19 cm3
Công thức tính bán kính mặt cầu đơn thuần
1. Mặt cầu ngoại tiếp khối chóp có cạnh bên vuông góc với đáy
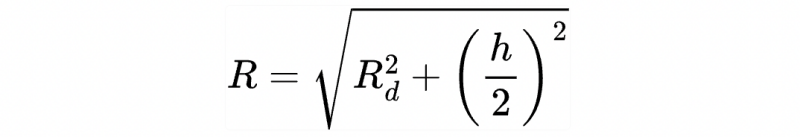
Trong đó:
- Rd là bán kính ngoại tiếp đáy.
- h là độ dài cạnh bên vuông góc với đáy.
Ví dụ: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 3a, BC = 4a, SA = 12a và SA vuông góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
Giải: Ta có

2. Khối tứ diện vuông (Trường hợp đặc biệt của công thức 1)
Khối từ diện vuông OABC có OA, OB, OC, đôi một vuông góc có:

3. Khối lăng trụ đứng có đáy là đa giác nội tiếp

Trong đó:
- Rd là bán kính ngoại tiếp đáy
- h là độ dài cạnh bên.

4. Tính khối tứ diện có những đỉnh là đỉnh của một khối lăng trụ đứng

5. Tính bán kính mặt cầu cho khối chóp có mặt bên vuông góc đáy

Ví dụ: Cho hình chóp S.ABCD có đáy là hình vuông, tam giác SAD đều cạnh √2a và nằm trong mặt phẳng vuông góc với mặt đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.

Một số bài tập về diện tích, thể tích hình cầu
Để tính thể tích khối cầu, chúng ta vận dụng ghi nhớ 3 bước như sau:
Bước 1: Phải thuộc công thức tính thể tích khối cầu, hãy ghi chúng ra giấy nháp, để tiện vận dụng công thức
Bước 2: Tìm bán kính hình cầu (quan trọng)
Có 2 trường hợp
- TH1: Đề bài toán đã cho bán kính thì chúng ta tới bước 3 (bước vận dụng công thức)
- TH2: Đề cho đường kính, chia đôi để được bán kính. Ví dụ, đường kính d = 20cm ⇒ bán kính r = 10cm.
Bước 3: Thay bán kính vừa tìm được vào công thức tính thể tích khối cầu V = ⁴⁄₃πr³, sau đó nhận đáp án đúng.
1. Bài tập tính thể tích của khối cầu có lời giải
Bài 1: Có đường tròn tâm O, bán kính là 9m. Hãy tính diện tích hình cầu?
Giải: Trước tiên, khi đã có bán kính của mặt cầu bạn tiến hành thay vào công thức Smặt cầu = 4 π.R^2, bạn được:
S = 4 x 3,14 x 9^2 = 1017.36 m2
Bài 2: Cho đường tròn tâm O, đường kính 2,5 cm. Hãy tính diện tích mặt cầu
Giải: Để tính diện tích hình cầu trường hợp này bạn cũng thay đường kính vào công thức Smặt cầu = π. d2, bạn được:
S = 3,14 x 2,5^2 = 19,625 cm2
Bài 3: Cho hình cầu có đường kính d = 6cm. Diện tích mặt cầu là:
A. 36π (cm2)
B. 9π (cm2)
C. 12π (cm2)
D. 36π (cm2)
Giải:
- Vì đường kính d= 6cm >> Nên bán kính hình cầu R= d/2 = 3cm
- Diện tích mặt cầu: S = 4πR^2 = 4π3^2 = 36 π (cm^2)
Bài 4: Tính thể tích khối cầu có đường kính d = 4 cm.
Giải:
Bán kính r = d/2 = 2 cm
Thể tích khối cầu là: V = ⁴⁄₃πr³ = 4/3.3,14.(2)³ = 33,49 cm³
Bài 5: Cho mặt cầu có thể tích V = 288π (cm3). Tính đường kính mặt cầu:
Ta có: V = ⁴⁄₃πr³ = 288π -> r = 6cm
Từ đó đường kính của mặt cầu là: d = 2r = 2.6 =12cm
Bài 6: Một mặt cầu có đường kính là d = 1,5 cm. Hãy tính thể tích mặt cầu?
Giải:

Bài 7: Thể tích khối cầu ngoại tiếp hình lập phương cạnh 3cm là?
Giải:

Câu 8: thắc mắc trong đề thi chuyên Trần Phú – Hải Phòng năm 2018

Câu 9: Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, SA vuông góc với mặt phẳng (ABC) và SA = a, AB = b, AC = c. Mặt cầu đi qua những đỉnh A, B, C, S có bán kính r bằng bao nhiêu?
Giải:


2. Bài tập tính thể tích của khối cầu không có lời giải

Câu 5: Cho tứ diện đều ABCD có cạnh đáy bằng a. Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng:

Câu 6: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng 45 độ. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD bằng:

Câu 7: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên bằng a. Bán kính của khối cầu ngoại tiếp hình chóp này bằng:

Câu 8: Thể tích khối cầu nội tiếp khối lập phương có cạnh bằng a là:

Câu 9: Cho hình lăng trụ tam giác đều có cạnh đáy và cạnh bên cùng bằng a. Diện tích của hình cầu ngoại tiếp hình lăng trụ này bằng:

Câu 10: Thể tích của khối cầu ngoại tiếp khối lập phương có cạnh bằng a là:

Câu 11: Gọi (S) là mặt cầu có tâm O và bán kính r, d là khoảng cách từ O tới mặt phẳng (P), d < r. lúc đó có bao nhiêu điểm chung giữa (S), (P)?
|
A. Vô số
|
B. 1
|
|
C. 0
|
D. 2
|
Câu 12: Cho tứ diện DABC, đáy ABC là tam giác vuông tại B, DA vuông góc với mặt đáy. Biết AB = 3a, BC = 4a, DA = 5a. bán kính mặt cầu ngoại tiếp hình chóp DABC có bán kính bằng:

Câu 13: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên đều bằng a. diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD bằng

Trên đây là những cách tính diện tích, thể tích hình cầu đơn thuần, nhanh chóng mà hàng ngũ Trường THPT Phạm Hồng Thái chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này những bạn hoàn toàn có thể tính diện tích, thể tích hình cầu một cách dễ dàng.
999+ tài khoản Chat GPT miễn phí, Acc OpenAI Free 100% đăng nhập thành công