Phương trình tham số. Cách viết phương trình tham số của đường thẳng
Phương trình tham số, phương trình chính tắc, vecto chỉ phương, hệ số góc, … là những kiến thức trọng tâm trong chương trình Toán 10, phân môn Hình học. Nhằm giúp các em nắm vững hơn lý thuyết về phương trình tham số và cách viết phương trình tham số của đường thẳng, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội đã chia sẻ bài viết sau đây.
I. CÁCH VIẾT PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG CỰC HAY
1. Phương trình tham số là gì ?
Phương trình tham số xác định bởi hệ các hàm số của một hoặc nhiều biến độc lập gọi là các tham số. Phương trình tham số thường được sử dụng để biểu diễn các tọa độ của các điểm thuộc đối tượng hình học như đường cong hoặc bề mặt, mà khi đó các đối tượng này được gọi là biểu diễn theo tham số hoặc tham số hóa.
Ví dụ, phương trình:
là dạng biểu diễn bằng tham số của đường tròn đơn vị, với t là tham số.
2. Vecto chỉ phương
– Cho đường thẳng d, vecto gọi là vecto chỉ phương của đường thẳng d nếu có giá song song hoặc trùng với d.
– là vecto chỉ phương của đường thẳng d thì
cũng là vecto chỉ phương của đường thẳng d.
– Vecto chỉ phương và vecto pháp tuyến vuông góc với nhau hay nói cách khác vecto chỉ phương của d là thì vecto pháp tuyến là
.
3. Cách viết phương trình tham số của đường thẳng
– Phương trình tham số của đường thẳng đi qua điểm A(x0; y0) nhận làm vecto chỉ phương, Ta có:
– Đường thẳng d đi qua điểm A(x0; y0), nhận là vecto chỉ phương, phương trình chính tắc của đường thẳng là
với (a; b ≠ 0)
– Nếu
4. Ví dụ:
Ví dụ 1: Viết phương trình đường thẳng d đi qua M( -2; 3) và có VTCP u→ = (1; -4) .
A. 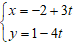 B.
B. 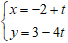 C.
C. 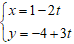 D.
D. 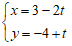
Lời giải
Đường thẳng (d) đi qua M(-2; 3) và có VTCP u→ = (1; -4) nên có phương trình
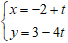
Chọn B.
Ví dụ 2. Đường thẳng d đi qua điểm M( 1; -2) và có vectơ chỉ phương u→ = (3; 5) có phương trình tham số là:
A. d: 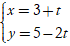 B. d:
B. d: 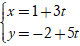 C. d:
C. d: 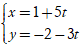 D. d:
D. d: 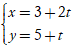
Lời giải
Đường thẳng d: 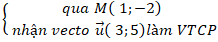
⇒ Phương trình tham số của đường thẳng d: 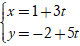 (t ∈ R)
(t ∈ R)
Chọn B.
II. BÀI TẬP VỀ PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG TRONG MẶT PHẲNG
1. Bài tập có đáp án
Bài 1: Đường thẳng đi qua hai điểm A(3; -7) và B( 1; -7) có phương trình tham số là:
A. 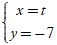 B.
B. 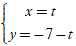 C.
C. 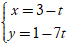 D.
D. 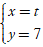
Lời giải
+ Ta có đường thẳng AB: 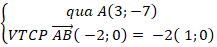
⇒ Phương trình AB: 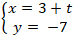
+ Cho t= – 3 ta được : M( 0; -7) thuộc đường thẳng AB.
⇒ AB: 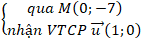
⇒ Phương trình tham số của AB : 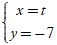
Chọn A.
Bài 2: Đường thẳng d đi qua gốc tọa độ O và có vectơ chỉ phương u→ = (-1; 2) có phương trình tham số là:
A. d: 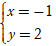 B. d:
B. d: 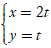 C. d:
C. d: 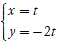 D. d:
D. d: 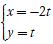
Trả lời:
Đường thẳng d: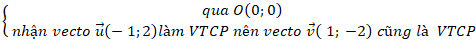
⇒ Phương trình tham số d: 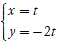 (t ∈ R)
(t ∈ R)
Đáp án: C
Bài 3: Cho 3 điểm A(-2; 1), B(-1; 5), C(-2; -3)
a. Viết phương trình tham số AB, AC.
b. Viết phương trình tham số đường trung trực cạnh BC.
c. Viết phương trình đường thẳng song song với AB và đi qua trung điểm của BC.
Hướng dẫn giải
a. Phương trình đường thẳng AB nhận làm vecto pháp tuyến
Phương trình tham số AB là: và phương trình chính tắc của d là:
Tương tự với đường thẳng AC có phương trình tham số là:
b. Đường trung trực của BC đi qua trung điểm của BC và nhận làm vecto pháp tuyến. Vậy vecto chỉ phương của đường thẳng trung trực là
Gọi M là trung điểm của BC khi đó:
Phương trình tham số đường trung trực BC là:
c. Do đường thẳng d tìm song song với AB nên
Theo câu b, trung điểm của BC là
Vậy phương trình tham số của d là:
Bài 4:
Viết phương trình đường thẳng y = ax + b biết
a) Đi qua 2 điểm A(-3,2), B (5,-4). Tính diện tích tam giác được tạo bởi đường thẳng và 2 trục tọa độ.
b) Đi qua A (3,1) song song với đường thẳng y = -2x + m -1.
Hướng dẫn giải
a. Gọi phương trình tổng quát là: y = ax + b
Do phương trình đường thẳng đi qua 2 điểm A, B nên ta có:
Vậy PT tổng quát cần tìm là:
Giao điểm của đường thẳng với trục Ox là:
Giao điểm của đường thẳng với trục Oy là:
b. Gọi phương trình tổng quát là: y = ax + b
Do đường thẳng song song với y = -2x + m -1
⇒ a = -2
Phương trình đường thẳng trở thành y = -2x + b
Mà đường thẳng qua điểm A(3; 1)
⇒ 1 = 3.(-2) + b
⇒ b = 7
Vậy phương trình tổng quát là: y = -2x + 7
Bài 5: Viết phương trình tham số, phương trình chính tắc của đường thẳng d trong các trường hợp sau:
a. Đường thẳng d đi qua 2 điểm A(-1;1), B(2; -1).
b. Đường thẳng d đi qua gốc tọa độ và song song với đường thẳng
Hướng dẫn giải
a. Ta có đường thẳng d đi qua 2 điểm A, B nên d nhận làm vecto chỉ phương.
Phương trình tham số của đường thẳng d là:
Phương trình chính tắc của đường thẳng là:
b. Ta có d song song với
Phương trình tham số của đường thẳng d là:
Phương trình chính tắc của d là:
Bài 6:Viết phương trình tham số, phương trình chính tắc của đường thẳng d trong các trường hợp sau:
a. Phương trình đi qua điểm A(1; 2) nhận làm vecto pháp tuyến.
b. Phương trình đi qua điểm B(0; 1) vuông góc với đường thẳng y = 2x + 1.
c. Phương trình song song với đường thẳng 4x + 3y – 1 = 0 và đi qua điểm M( 0, 1).
Hướng dẫn giải
a. Gọi điểm M(x, y) thuộc d ta có:
Phương trình chính tắc là:
b. Ta có đường thẳng y = 2x + 1 có vecto pháp tuyến
Do đường thẳng d vuông góc với đường thẳng y = 2x + 1 nên VTPT của y = 2x + 1 là VTCP
của d
Ta có phương trình tham số của d là:
2. Bài luyện tập thêm
Bài 1:
1. Cho 3 điểm A(-4;1), B(0;2), C(3;-1).
a) Viết phương trình tham số của các đường thẳng AB, BC, CA.
b) Gọi M là trung điểm của BC. Viết phương trình tham số của đường thẳng AM.
2. Cho tam giác ABC có A(1;4); B(-9;0); C(7;1)
a) Viết phương trình tham số của đường thẳng AB, BC, CA.
b) Viết phương trình tham số đường trung tuyến của tam giác ABC.
Bài 2: Cho 2 đường thẳng
a) Tìm tọa độ giao điểm A của d1 và d2
b) Viết phương trình tham số và phương trình tổng quát của:
+ Đường thẳng đi qua A và vuông góc với d1
+ Đường thẳng đi qua A và song song với d2
Bài 3: Cho tam giác ABC có A(-2; 1), B(-1; 5), C(2; 3)
a. Viết phương trình tham số các cạnh AB, BC, AC.
b. Viết phương trình đường trung tuyến AM, CP với M, P lần lượt là trung điểm của cạnh BC, AB.
c. Viết phương trình tham số đường cao AH.
d. Viết phương trình đường thẳng đi qua A và song song với BC.
e. Đường thẳng đi qua B và vuông góc với y = 2x – 3.
Bài 4: Viết phương trình tham số, phương trình chính tắc (nếu có) trong các trường hợp sau:
a. Đường thẳng đi qua 2 điểm A(-2; 0), B(1; 3).
b. Đường thẳng đi qua M(3; -2) song song với đường thẳng 2x + 5y – 4 = 0.
c. Đường thẳng có hệ số góc k = 1 đi qua điểm D(-1; -1).
d. Đường thẳng d đi qua gốc tọa độ và vuông góc với đường thẳng x – y – 1 = 0.
Vậy là chúng tôi đã giới thiệu đến quý bạn đọc lý thuyết về phương trình tham số và cách viết phương trình tham số của đường thẳng cực hay. Hi vọng, sau khi chia sẻ cùng bài viết, bạn nắm vững hơn phần kiến thức vô cùng quan trọng này. Xem thêm cách tìm Vectơ chỉ phương của đường thẳng tại đường link này nhé !