Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
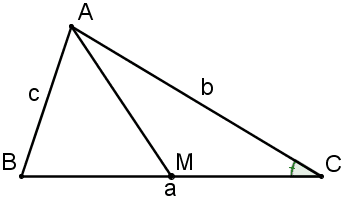
Ví dụ. Cho tam giác  , có
, có 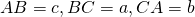 và
và  là trung điểm của
là trung điểm của  . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến  theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.

* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn  do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.

* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.

* Thay (2) vào (1), rồi rút gọn ta có kết quả

III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:


Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:

Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:
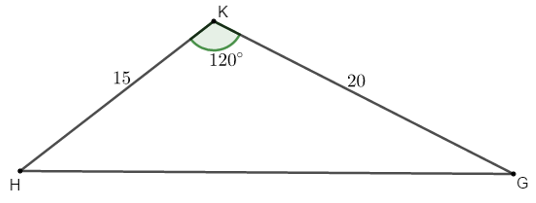
a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:

Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:


Bài 5: Cho tam giác ABC, có  . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:

Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

Do AD là phân giác của góc 
Đáp án A
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:
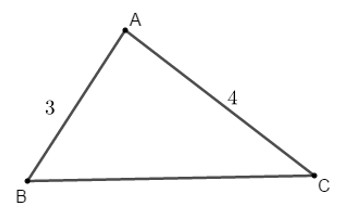

Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !
Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Ví dụ. Cho tam giác  , có
, có  và
và  là trung điểm của
là trung điểm của  . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến  theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.
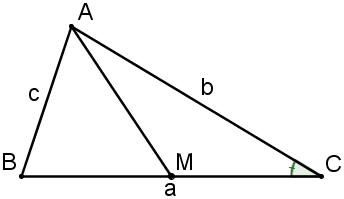
* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn  do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
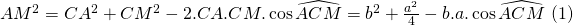
* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.
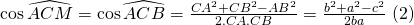
* Thay (2) vào (1), rồi rút gọn ta có kết quả
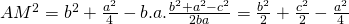
III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:


Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:

Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:
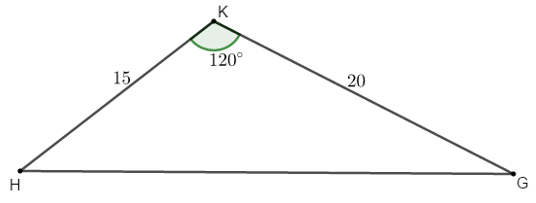
a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:

Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:
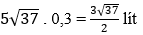

Bài 5: Cho tam giác ABC, có 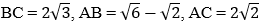 . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:
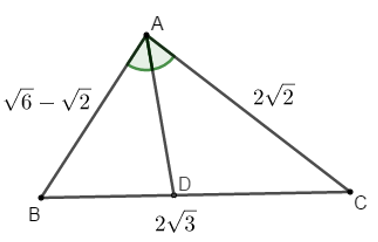
Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

Do AD là phân giác của góc 
Đáp án A
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:


Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !
Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Ví dụ. Cho tam giác  , có
, có  và
và  là trung điểm của
là trung điểm của  . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến  theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.

* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn 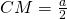 do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.

* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.

* Thay (2) vào (1), rồi rút gọn ta có kết quả

III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:
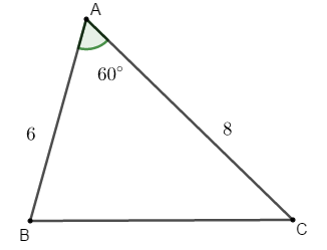

Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:
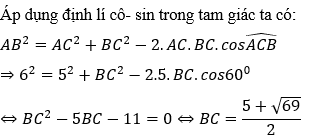
Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:

a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:

Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:


Bài 5: Cho tam giác ABC, có  . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:

Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

Do AD là phân giác của góc 
Đáp án A
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:


Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !
Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Ví dụ. Cho tam giác  , có
, có  và
và  là trung điểm của
là trung điểm của  . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến  theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.
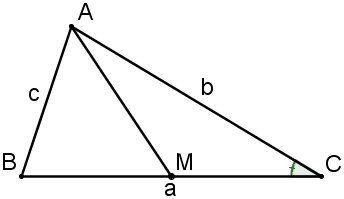
* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn  do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
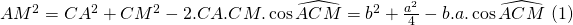
* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.

* Thay (2) vào (1), rồi rút gọn ta có kết quả

III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:


Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:

Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:

a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:
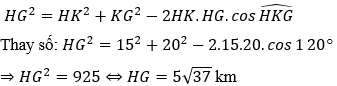
Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:


Bài 5: Cho tam giác ABC, có  . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:

Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

Do AD là phân giác của góc 
Đáp án A
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:


Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !
Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Ví dụ. Cho tam giác  , có
, có  và
và  là trung điểm của
là trung điểm của  . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến  theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.
* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn  do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.

* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.

* Thay (2) vào (1), rồi rút gọn ta có kết quả

III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:


Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:

Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:

a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:

Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:


Bài 5: Cho tam giác ABC, có  . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:

Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

Do AD là phân giác của góc 
Đáp án A
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:


Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !
Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Ví dụ. Cho tam giác  , có
, có 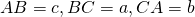 và
và  là trung điểm của
là trung điểm của 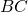 . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến  theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.

* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn  do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.

* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.

* Thay (2) vào (1), rồi rút gọn ta có kết quả

III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:

Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:

Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:

a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:

Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:


Bài 5: Cho tam giác ABC, có  . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:

Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

Do AD là phân giác của góc 
Đáp án A
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:

Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !
Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Ví dụ. Cho tam giác 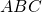 , có
, có  và
và 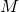 là trung điểm của
là trung điểm của  . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến  theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.

* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn  do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.

* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.

* Thay (2) vào (1), rồi rút gọn ta có kết quả

III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
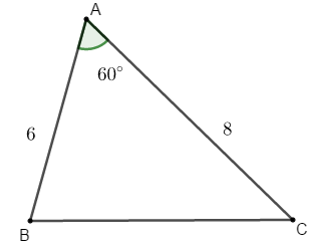
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:


Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:

Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:

a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:

Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:
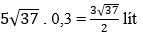

Bài 5: Cho tam giác ABC, có  . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:
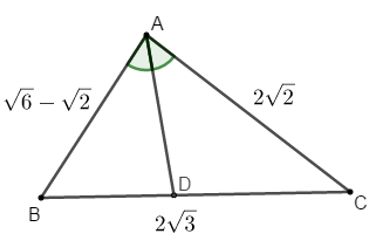
Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

Do AD là phân giác của góc 
Đáp án A
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:


Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !
Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Ví dụ. Cho tam giác  , có
, có  và
và  là trung điểm của
là trung điểm của  . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến 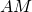 theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.

* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn 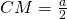 do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.

* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.

* Thay (2) vào (1), rồi rút gọn ta có kết quả

III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
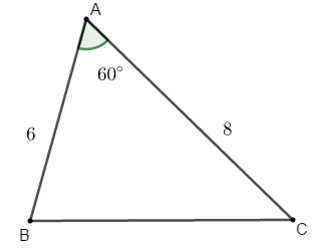
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:

Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:
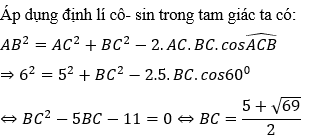
Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:
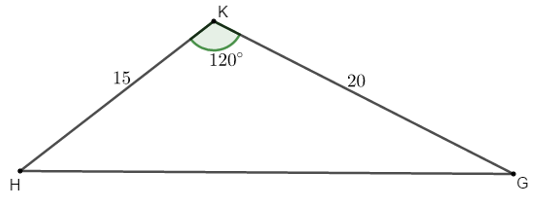
a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:

Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:
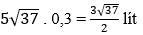

Bài 5: Cho tam giác ABC, có  . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:

Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:

Do AD là phân giác của góc 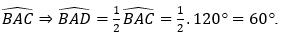
Đáp án A
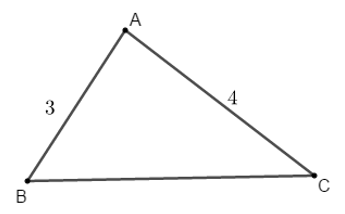
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:


Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !
Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay
Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé !
I. ĐỊNH LÍ CÔSIN (ĐỊNH LÍ HÀM COS) TRONG TÁM GIÁC
1. Sự ra đời của định lí Côsin
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.
2. Định lý Côsin trong tam giác
Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.
3. Chứng minh định lý Côsin
Để chứng minh định lý này bạn có thể áp dụng phương pháp dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.


4. Hệ quả định lý Côsin

Như vậy hệ quả của định lý cosin cho thấy nếu biết được độ dài của 3 cạnh ta sẽ tính được số đo của các góc. Hay có thể hiểu đơn giản rằng định lý cosin sẽ giúp ta tính được độ dài của cạnh thì hệ quả của định lý này sẽ giúp chúng ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin có thể giúp ta tìm được độ dài các đường trung tuyến theo ba cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì :
ma2=2b2+c2 -a24mb2=2a2+c2 -b24mc2=2a2+b2 -c24
II. CÁCH VẬN DỤNG ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Ví dụ. Cho tam giác  , có
, có  và
và  là trung điểm của
là trung điểm của  . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến  theo
theo  và
và  .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.

* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM.
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn  do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.

* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.

* Thay (2) vào (1), rồi rút gọn ta có kết quả
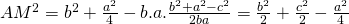
III. BÀI TẬP VỀ ĐỊNH LÍ CÔSIN
Bài 1: Cho tam giác ABC có  . Tính BC.
. Tính BC.
Hướng dẫn giải:


Bài 2: Cho tam giác ABC có cách cạnh  . Tính cosA và góc A.
. Tính cosA và góc A.
Hướng dẫn giải:


Bài 3: Cho tam giác ABC có AB = 6cm; AC = 5cm và  . Tính BC?
. Tính BC?
Hướng dẫn giải:

Bài 4: Một ô tô muốn đi từ địa điểm H đến địa điểm G, nhưng giữa H và G là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ H lên K (ô tô leo dốc lên núi) và từ K đến G (ô tô xuống núi). Các đoạn đường tạo thành tam giác HKG với HK = 15km, KG = 20km và  . Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
. Giả sử cứ chạy 1km, ô tô tiêu thụ hết 0,3 lít xăng. Giá thành xăng hiện nay là 13050 đồng một lít xăng.
a, Ô tô đi từ H đến G hết bao nhiêu tiền xăng?
b, Nếu người ta đào một đường hầm xuyên núi chạy thẳng từ H đến G thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu kinh phí?
Hướng dẫn giải:

a, Tổng quãng đường mà ô tô phải đi là:
S = HK + KG = 15 + 20 = 35 km
Ô tô đi hết quãng đường tiêu thụ hết số lít xăng là:
35 . 0,3 = 10,5 lít
Ô tô đi từ H đến G hết số tiền xăng là:
10,5 . 13050 = 137025 đồng
b, Ô tô đi thẳng từ H đến G
Áp dụng định lý Cô-sin vào tam giác HKG ta có:
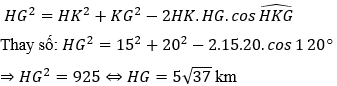
Do đó ô tô phải đi quãng đường là 5√37km và tiêu thụ hết số lít xăng là:


Bài 5: Cho tam giác ABC, có  . AD là tia phân giác của góc
. AD là tia phân giác của góc
A. Tính góc BAD
A. 60°
B. 90°
C. 45°
D. 75°
Hướng dẫn giải:

Áp dụng hệ quả định lý Cô-sin trong tam giác ABC, ta có:
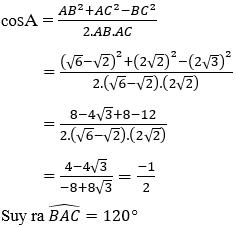
Do AD là phân giác của góc 
Đáp án A
Bài 6: Cho tam giác ABC có AB = 3, AC = 4 và  Tính BC.
Tính BC.

Hướng dẫn giải:


Đáp án D
Vậy là các bạn vừa được tìm hiểu Định lí Côsin và Cách vận dụng định lý Côsin trong tam giác cực hay và nhiều kiến thức liên quan khác. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu hữu ích phục vụ quá trình dạy và học tốt hơn. Xem thêm công thức tính tích vô hướng của hai vectơ nữa bạn nhé !