Công thức tính thể tích khối trụ & các dạng bài tập có đáp án Chính Xác

Khối trụ là gì? Công thức tính thể tích khối trụ ra sao và nó có những dạng bài tập thế nào là những mạch kiến thức Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giới thiệu tới quý thầy cô cùng các bạn học sinh trong bài viết này. Đây là phần kiến thức Hình học 12 rất quan trọng, có hầu hết trong các đề thi. Hãy chia sẻ để có thêm nguồn tư liệu hữu ích bạn nhé !

I. KIẾN THỨC CHUNG

1. Thể tích là gì?

Thể tích của một hình, của một vật, hay một dung tích là một lượng không gian vật áy chiếm, là giá trị cho biết hình đó chiếm bao nhiêu phần trong không gian ba chiều.

Có thể tưởng tượng thể tích của một hình là lượng nước (hoặc không khí, cát,…) mà hình đó có thể chứa khi được làm đầy bằng các vật thể ở trên.

Đơn vị đo thể tích là mét khối; Ký hiệu là m³

2. Hình trụ là gì?

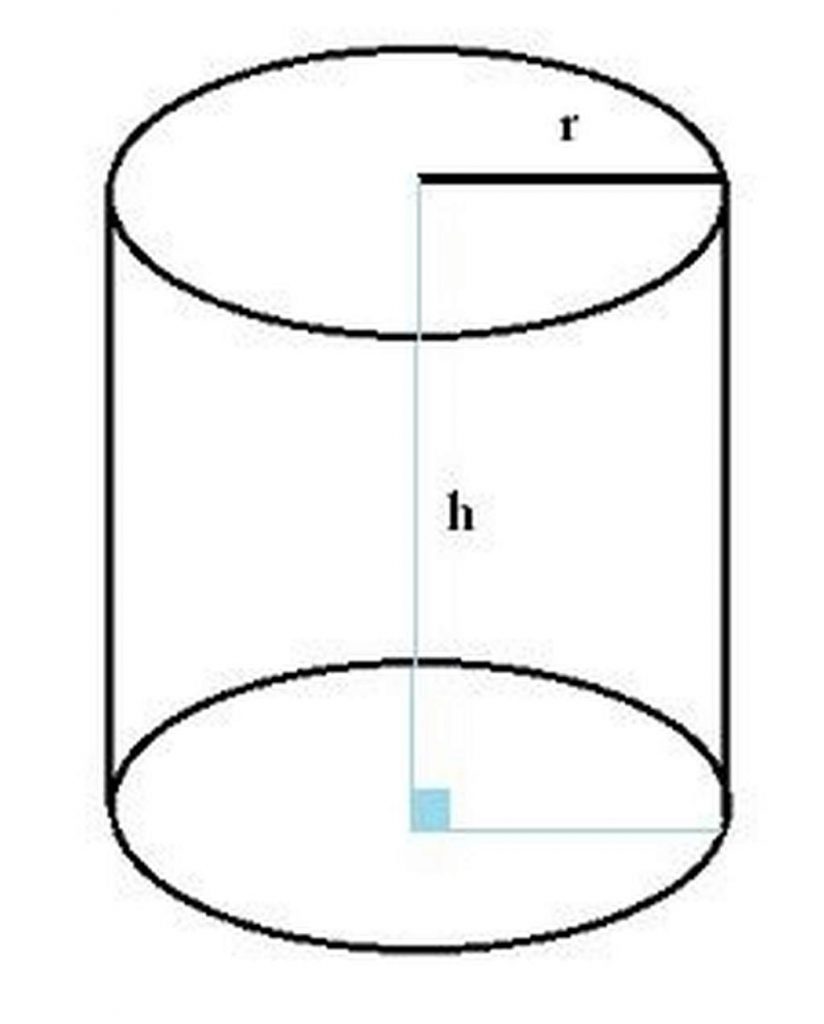
Có nhiều cách để giải thích hình trụ là gì, nhưng nhìn chung, chúng ta có thể hiểu khái niệm hình trụ như sau:

Khi quay hình chữ nhật một vòng quanh một cạnh cố định ta thu được một hình trụ. Hình trụ là hình được giới hạn bởi mặt trụ và hai đường tròn bằng nhau (có bán kính là r), 2 hình tròn này được gọi là đáy của hình trụ, h là chiều cao của hình trụ, vuông góc với 2 mặt đáy.

3. Khối trụ là gì?

Khối trụ là hình trụ cùng với phần bên trong của hình trụ đó.

Thể tích khối trụ là lượng không gian mà hình trụ chiếm.

4. Thể tích khối trụ là gì ?

Thể tích khối trụ là thể tích khi mà diện tích đáy được đặt dồn lên nhau cho đến hết chiều cao của khối trụ. Là lượng không gian được chiếm giữ một khối trụ nhất định. Lượng không gian mà khối trụ đó chiếm được gọi là thể tích khối trụ.

II. CÔNG THỨC TÍNH THỂ TÍCH KHỐI TRỤ

1. Công thức tính thể tích hình trụ tròn

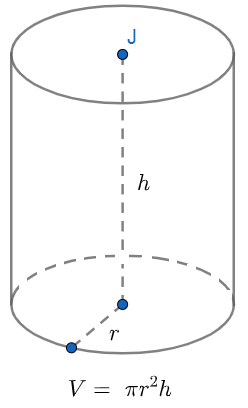
Muốn tính thể tích của hình trụ tròn, ta lấy chiều cao nhân với bình phương độ dài bán kính hình tròn mặt đáy hình trụ và số pi.

Trong đó:

• V là thể tích hình trụ.
• r là bán kính hình trụ.
• h là chiều cao, khoảng cách giữa 2 đáy của hình trụ.
• Đơn vị thể tích: mét khối (m³)

Ví dụ:

Cho khối trụ (H) có bán kính đáy bằng 3 cm và chiều cao bằng đường kính đáy. Tính thể tích khối trụ đã cho.

Lời giải:

Chiều cao của khối trụ là 6 (cm).

Vậy thể tích khối trụ là V=πr²h= π.3².6=54 (cm³).

2. Công thức tính thể tích hình lăng trụ

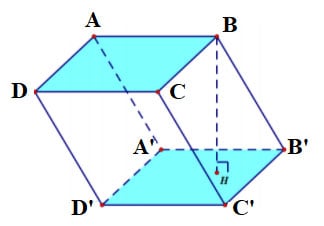
Một đa giác có hai mặt đáy song song và bằng nhau, mặt bên là hình bình hành thì đa giác đó gọi là hình lăng trụ.

Công thức tính thể tích hình lăng trụ đứng:

V = B.h

Trong đó

• V là thể tích khối lăng trụ (đơn vị m3)
• B là diện tích đáy (đơn vị m2)
• h là chiều cao khối lăng trụ (đơn vị m)

Ví dụ:

Cho khối lăng trụ đứng ABC.A′B′C′có đáy là tam giác ABC có ˆBAC=60∘,AB=3a và AC=4a.AC=4a.Gọi M là trung điểm của B′C′, biết khoảng cách từ M đến mặt phẳng (B′AC) bằng 3a√15/10. Thể tích khối lăng trụ đã cho là:

A. a³

B. 9a³ 

C. 4a³

D. 27a³

^{Đáp án: chọn D}

^{2.1 Diện tích xung quanh của hình trụ}

Diện tích xung quanh hình trụ được tính như sau:

S_xq = 2 . π . r . h

^{2.2 Diện tích toàn phần của hình trụ}

Stp = 2 . π . r . h + 2 . π . r²

III. CÁC DẠNG BÀI TOÁN VỀ THỂ TÍCH KHỐI TRỤ, HÌNH TRỤ

Dạng 1: Cho biết bán kính đáy và chiều cao tính thể tích khối trụ

Ví dụ: Cho khối trụ có đáy là hình tròn ngoại tiếp tam giác đều cạnh a. Chiều cao khối trụ bằng 3a. Tính thể tích khối trụ đã cho.

Lời giải:

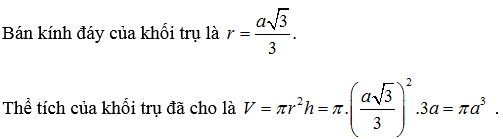
Dạng 2: Cho biết thể tích khối trụ và bán kính đáy tính chiều cao

Ví dụ:

Biết khối trụ có thể tích V=12π và chu vi một đáy là C=2π. Tính chiều cao của khối trụ đã cho.

Lời giải:

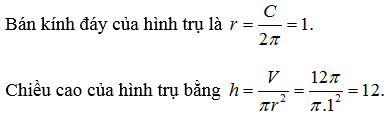
Dạng 3: Cho biết thể tích khối trụ và chiều cao tính bán kính đáy

Ví dụ: Cho khối trụ có thể tích bằng πa³, chiều cao 2a. Tính bán kính đáy của khối trụ.

Lời giải:

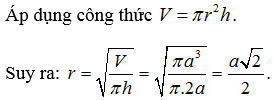
IV: BÀI TẬP VỀ THỂ TÍCH KHỐI TRỤ, HÌNH TRỤ

1. Bài tập có lời giải:

Bài 1: 

Tính thể tích của hình trụ biết bán kính hai mặt đáy bằng 7,1 cm; chiều cao bằng 5 cm.

Giải:

Ta có V=πr²h

thể tích của hình trụ là: 3.14 x (7,1)² x 5 = 791,437 (cm³)

Bài 2: Một hình trụ có diện tích xung quanh là 20π cm² và diện tích toàn phần là 28π cm². Tính thể tích của hình trụ đó.

Giải:

Diện tích toàn phần hình trụ là Stp = Sxq + Sđ = 2πrh + 2πr²

Suy ra, 2πr² = 28π – 20π = 8π

Do đó, r = 2cm

Diện tích xung quanh hình trụ là Sxq = 2πrh

<=> 20π = 2π.2.h
<=> h = 5cm

Thể tích hình trụ là V = πr²h = π.22.5 = 20π cm³

Bài 3: Một hình trụ có chu vi đáy bằng 20 cm, diện tích xung quanh bằng 14 cm². Tính chiều cao của hình trụ và thể tích của hình trụ.

Lời giải: Chu vi đáy của hình trụ là chu vi của hình tròn = 2rπ = 20 cm

Diện tích xung quanh của hình trụ: Sxq = 2πrh= 20 x h = 14
→ h = 14/20 = 0,7 (cm)

2rπ = 20 => r ~ 3,18 cm

Thể tích của hình trụ: V = π r² x h ~ 219,91 cm³

2. Bài luyện tập thêm:

Bài tập 1. Một bể nước hình trụ có diện tích mặt đáy B = 2 m2 và đường cao h = 1 m. Thể tích của bể nước này bằng bao nhiêu?

Bài tập 2. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a = 2 cm và chiều cao là h = 3 cm. Hãy tính thể tích hình lăng trụ này

Bài tập 3. Cho hình lăng trụ tam giác đều có các cạnh đều bằng 2a. Tính thể tích khối lăng trụ đều này.

Bài tập 4. Cho khối trụ (H) có bán kính đáy bằng 3 cm và chiều cao bằng đường kính đáy. Tính thể tích khối trụ đã cho.

Bài tập 5. Cho khối trụ có đáy là hình tròn ngoại tiếp tam giác đều cạnh a. Chiều cao khối trụ bằng 3a. Tính thể tích khối trụ đã cho.

Bài tập 6. Cho khối trụ có thể tích bằng π x a³, chiều cao 2a. Tính bán kính đáy của khối trụ.

Bài tập 7. Biết khối trụ có thể tích V=12π  và chu vi một đáy là C=2π . Tính chiều cao của khối trụ đã cho.

Bài tập 8. Tính thể tích khối lăng trụ tam giác đều có cạnh đáy bằng 2a, cạnh bên bằng a

Trên đây Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội đã giới thiệu đén bạn Công thức tính thể tích khối trụ, hình trụ và nhiều công thức  cùng dạng bài tập liên quan khác. Hi vọng, đây sẽ là nguồn tư liệu quý cho thầy cô cũng như các bạn học sinh. Xem thêm công thức tính thể tích hình hộp chữ nhật bạn nhé !