Công thức tính góc giữa 2 vectơ trong mặt phẳng và trong không gian
Việc tính góc giữa 2 vectơ trong mặt phẳng và trong không gian là phần kiến thức Toán phổ thông vô cùng quan trọng. Nhằm giúp các em có thêm nhiều kiến thức, kỹ năng hay trong việc giải toán dang này, Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội đã chia sẻ công thức tính góc giữa 2 vectơ trong mặt phẳng và trong không gian và nhiều dạng bài tập thường gặp. Bạn tìm hiểu nhé !
I. GÓC GIỮA HAI VECTƠ TRONG KHÔNG GIAN LÀ GÌ ?
Góc giữa 2 véc tơ trong không gian được định nghĩa hoàn toàn tương tự góc giữa hai véc tơ trong mặt phẳng.
Nếu ít nhất một trong hai véc tơ là véc tơ không thì góc giữa hai véc tơ đó không xác định (đôi khi một số tài liệu cũng coi góc giữa hai véc tơ đó bằng 0).Còn trong trường hợp cả 2 véc tơ đều khác véc tơ không thì ta tiến hành đưa về chung gốc.
Cụ thể:

Rõ ràng từ định nghĩa trên ta suy ra được góc giữa hai véc tơ có một số tính chất. Chẳng hạn:
Góc giữa hai véc tơ bằng 0º khi và chỉ khi hai véc tơ đó cùng chiều.Góc giữa hai véc tơ bằng 180º khi và chỉ khi hai véc tơ đó ngược chiều.Góc giữa hai véc tơ bằng 90º khi và chỉ khi hai véc tơ đó vuông góc.
II. CÁCH TÍNH GÓC GIỮA HAI VECTƠ TRONG MẶT PHẲNG OXY
1. Công thức
Cho hai véc-tơ và véc-tơ
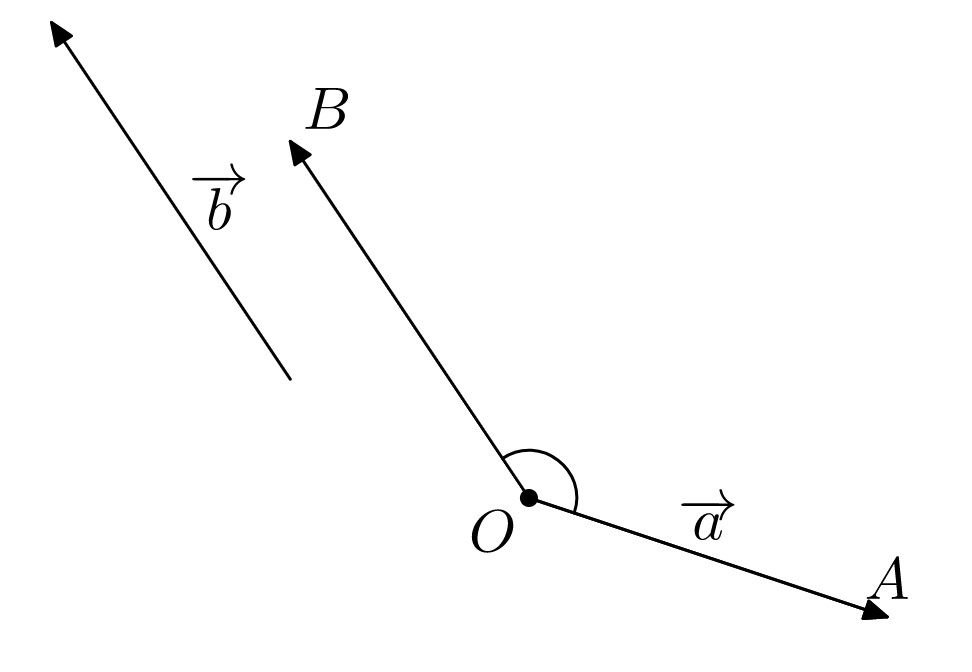
đều khác 0. Từ một điểm O bất kỳ, dựng vectơ OA = véc-tơ
và dựng vectơ OB = véc-tơ
. Khi đó góc AOB gọi là góc giữa hai véc-tơ
và véc-tơ
.
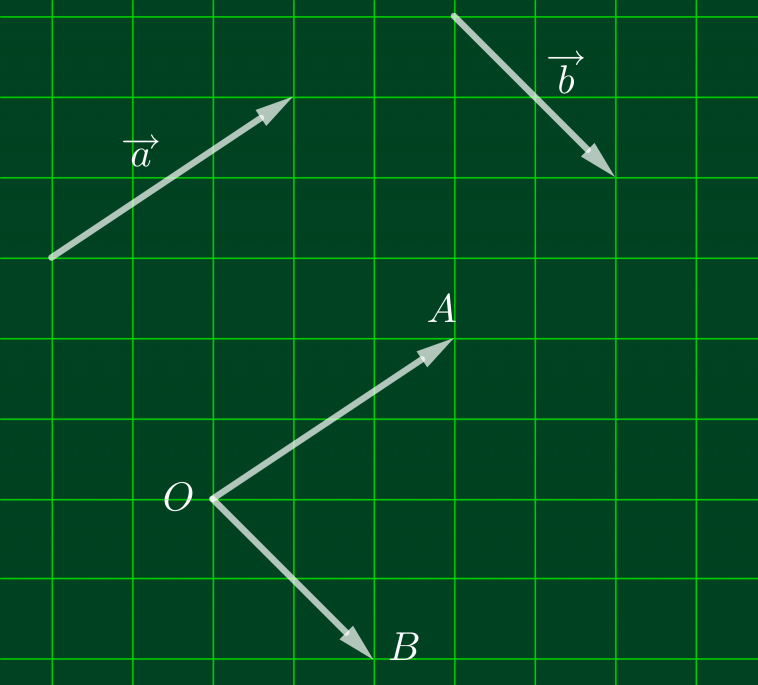
Nhận xét.
- Trong định nghĩa thì điểm O được lấy tuỳ ý. Tuy nhiên, trong lúc giải toán ta có thể chọn O trùng với điểm gốc của vectơ a hoặc vectơ b cho đơn giản.
- Hiểu một cách đơn giản, để xác định góc giữa hai véc-tơ ta thay thế hai vectơ đã cho bởi hai vecto mới có chung điểm gốc.
 2. Tính chất góc giữa hai véc-tơ trong mặt phẳng
2. Tính chất góc giữa hai véc-tơ trong mặt phẳng
- Góc giữa hai vecto bất kì luôn nằm trong đoạn từ 00 đến 1800.
- Góc giữa hai véc tơ bằng 00 khi và chỉ khi hai véc tơ đó cùng chiều.
- Góc giữa hai véc tơ bằng 1800 khi và chỉ khi hai véc tơ đó ngược chiều.
- Góc giữa hai véc tơ bằng 900 khi và chỉ khi hai véc tơ đó vuông góc.
III. CÁCH TÍNH GÓC GIỮA HAI VECTƠ TRONG KHÔNG GIAN
(Áp dụng trong hệ tọa độ) Tính cos góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ.
Sử dụng công thức sau:
Cho hai vectơ 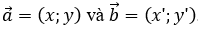 . Khi đó
. Khi đó
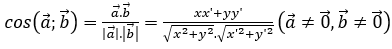
Chú ý: Góc giữa hai vectơ thuộc [0°;180°]
IV. CÁC DẠNG BÀI TẬP THƯỜNG GẶP
Bài 1: Cho các vectơ 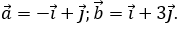 Tính góc giữa hai vectơ
Tính góc giữa hai vectơ 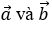 .
.
Hướng dẫn giải:
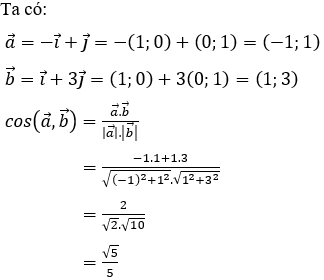
Vậy góc giữa hai vectơ 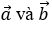 là góc α ∈ [0°;180°] thỏa mãn
là góc α ∈ [0°;180°] thỏa mãn 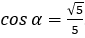 .
.
Bài 2: Trong mặt phẳng tọa độ Oxy, cho hai vectơ 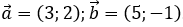 . Tính góc giữa hai vectơ
. Tính góc giữa hai vectơ 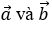 .
.
A. 45°
B. 60°
C. 90°
D. 30°
Hướng dẫn giải:

Đáp án A
Bài 3: Cho hai vectơ 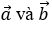 có độ dài bằng 1 và thỏa mãn điều kiện
có độ dài bằng 1 và thỏa mãn điều kiện 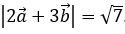 . Tính góc giữa hai vectơ
. Tính góc giữa hai vectơ 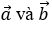 .
.
A. 60°
B. 30°
C. 120°
D. 150°
Hướng dẫn giải:
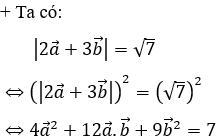
Vì 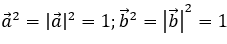 (bình phương vô hướng bằng bình phương độ dài)
(bình phương vô hướng bằng bình phương độ dài)

Đáp án C
Bài 4: Cho tam giác ABC vuông cân tại A. Tính góc giữa hai vectơ:
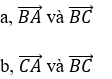
Hướng dẫn giải:
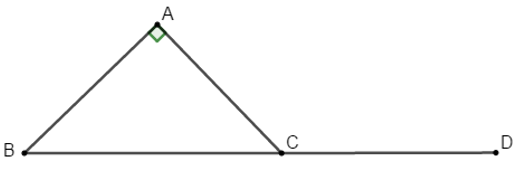

– Nhớ lại khái niệm hai vectơ bằng nhau ở chương 1: Hai vectơ bằng nhau khi chúng cùng hướng và cùng độ dài.
– Trên tia đối của tia CB lấy D sao cho CB = CD.
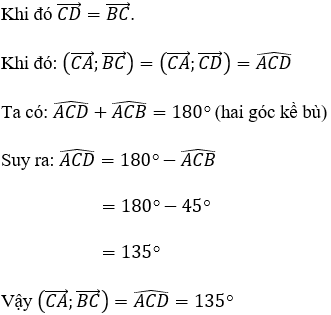
Bài 5: Cho các vectơ 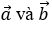 thỏa mãn
thỏa mãn 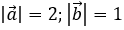 . Góc giữa vectơ
. Góc giữa vectơ 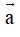 và vectơ
và vectơ 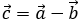 là
là
A. 30°
B. 60°
C. 90°
D. 120°
Hướng dẫn giải:
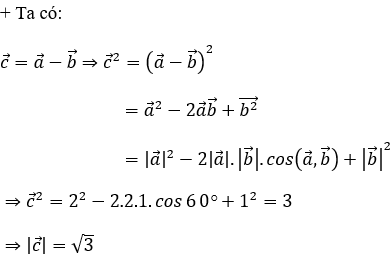
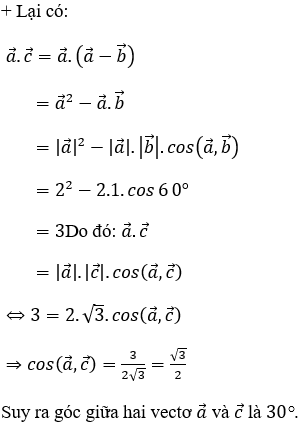
Đáp án A
Trên đây Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội đã giới thiệu đến các bạn lý thuyết về góc giữa 2 vectơ và công thức tính góc giữa 2 vectơ trong mặt phẳng và trong không gian cực hay. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu giúp các bạn dạy và học tốt hơn. Xem thêm cách tìm Vectơ chỉ phương của đường thẳng tại đường link này bạn nhé !