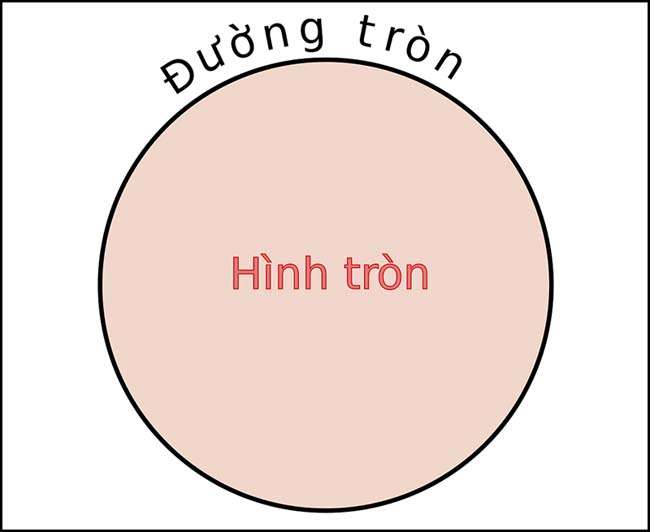
Định nghĩa về hình tròn

Diện tích hình tròn được nghiên cứu bởi những người Hy Lạp cổ đại. Vào thế kỷ thứ 5 trước Công nguyên, người ta tìm thấy rằng diện tích của hình tròn tỷ lệ thuận với bình phương bán kính của nó.

Hình tròn là vùng mặt phẳng bị giới hạn bởi 1 đường tròn. Tâm, bán kính cũng như chu vi của hình tròn chính là tâm và bán kính của đường tròn bao quanh.

Đường tròn là vòng bao quanh hình tròn. tất cả các điểm trên một mặt phẳng đều cách đều điểm đã cho trước và bằng 1 khoảng cách cho trước. Điểm cho trước là tâm và khoảng cách cho trước là bán kính đường tròn.

Cách để Tính diện tích hình tròn

Công thức tính diện tích hình tròn bằng bình phương bán kính nhân với Pi.

Hay diện tích hình tròn cũng được tính theo công thưc là bình phương đường kính nhân với Pi rồi chia cho 4.

Trong đó:

• S: diện tích hình tròn
• r: bán kính hình tròn
• d: đường kính hình tròn
• 3,14: chính là hằng số π (Pi)

Nhận xét: Để tính được S ta cần phải biết bán kính của hình tròn đó.

Một số đại lượng giúp ta tìm ra giá trị bán kính của hình tròn và S của nó:

• Đường kính hình tròn: d = 2R => R = d/2 => S = πd²/4
• Chu vi hình tròn: C = πd = 2πR => R = C/2π => S = C²/4π

– Ý nghĩa

Công thức tính diện tích hình tròn giúp bạn tính được toàn bộ diện tích bề mặt nằm bên trong vòng tròn.

– Ví dụ: Ta có một hình tròn C có đường kính d=10cm. Hỏi diện tích hình tròn C bằng bao nhiêu?
Áp dụng cách tính: diện tích hình tròn C ta có: r = 1/2 x d = 1/2×10 = 5cm
Suy ra: S = Pi x r² = 5 x (3,14)² = 49,298 cm2

Xác định bán kính hình tròn

Khi bạn có đường kính (d) của hình tròn, bạn có thể tìm bán kính (r) bằng công thức d = 2 x r. Bán kính của hình tròn là khoảng cách từ tâm của hình tròn đến bất kỳ điểm nào trên cạnh của hình tròn. Bán kính cũng bằng một nửa đường kính. Nếu đường kính của bạn là một số đơn giản, bạn có thể tính bán kính trong đầu. Nếu không, sắp xếp lại công thức để tìm r (r = d/2) và giải.

Dùng bán kính để tìm diện tích

Độ dài bán kính được tính từ tâm hình tròn cho đến cạnh của nó. Dù bạn đo theo bất cứ cách nào, bán kính của một hình tròn đều như nhau. Bạn có thể hiểu theo nghĩa khác là bán kính chính bằng một nửa đường kính hình tròn. 

Khi đề bài cho ta sẵn độ dài bán kính, ví dụ như là 3cm. Chỉ cần áp dụng công thức tính diện tích, lấy bán kính = 3cm bình phương lên ra 9 rồi nhân với số Pi 3,14 là ra kết quả diện tích của hình tròn là 28,26 (cm vuông).

Chú ý kết quả cần ghi đơn vị chính xác, nếu đề bài cho bán kính đơn vị là cm thì kết quả diện tích sẽ có đơn vị là cm vuông, tương tự nếu là mét thì khi ghi kết quả cho diện tích, chúng ta cần ghi mét vuông vào đó. 

Bán kính của hình tròn

Bán kính là độ dài từ tâm đến cạnh của hình tròn. Dù bạn đo theo bất cứ hướng nào, bán kính vẫn là như nhau. Bán kính cũng chính là một nửa đường kính hình tròn. Đường kính là đoạn thẳng đi qua tâm và nối hai phía đối diện của hình tròn với nhau.

• Đề bài thường cho sẵn bán kính. Hơi khó để xác định chính xác tâm của hình tròn, trừ khi nó đã được cho sẵn trên hình vẽ đề bài cung cấp.
• Trong ví dụ này, giả sử đề bài cho bạn bán kính hình tròn là 6 cm.

Bình phương bán kính

Công thức tính diện tích hình tròn là , trong đó biến  đại diện cho bán kính. Biến này được bình phương lên.

• Đừng nhầm lẫn và bình phương toàn bộ biểu thức.
• Ví dụ: một hình tròn có bán kính, , ta có .

Nhân với pi

Pi là một hằng số toán học đại diện cho tỉ lệ giữa chu vi và đường kính hình tròn. Nó được ký hiệu bằng chữ cái Hy lạp . Sau khi làm tròn theo số thập phân,  gần bằng 3,14. Giá trị số thập phân đúng thật ra còn kéo dài vô tận. Thông thường, để trình bày diện tích hình tròn một cách chính xác, chúng ta sẽ viết đáp số theo ký hiệu .

• Với ví dụ về hình tròn có bán kính là 6 cm, diện tích sẽ được tính như sau:
  • 
  • 
  •  hay 

Trình bày đáp án

Nhớ rằng khi tính toán diện tích, đơn vị phải luôn được trình bày kèm theo dấu “bình phương” (đọc là vuông). Nếu bán kính được tính bằng xăng-ti-mét, diện tích sẽ là xăng-ti-mét vuông. Nếu bán kính được tính theo mét, diện tích sẽ là mét vuông. Bạn cũng cần biết đề yêu cầu chúng ta trình bày đáp số như thế nào: theo ký hiệu {displaystyle pi } hay tính ra số thập phân làm tròn? Nếu như không biết, hãy trình bày theo cả hai cách.

• Đối với hình tròn có bán kính 6 cm, diện tích sẽ là 36 cm² hay 113,04 cm².

Tính diện tích theo đường kính

– Ví dụ: Ta có hình tròn C với đường kính là 8cm. Tính diện tích hình tròn C.
Áp dụng cách tính, S = Pi x (d/2)^2 = 50,265cm2

Đo hay viết lại đường kính

Trong một số bài toán hay tình huống, bạn sẽ không biết được bán kính. Thay vào đó, bạn sẽ chỉ biết độ dài đường kính của hình tròn. Nếu đường kính được vẽ trong sơ đồ bài toán, bạn có thể dùng thước để đo. Hoặc, bài toán sẽ cho sẵn độ dài của đường kính.

• Giả sử, bạn có hình tròn với đường kính 20 cm.

Chia đôi đường kính

Nhớ rằng đường kính dài gấp đôi bán kính. Vì thế, bất kể đề bài cho bạn giá trị đường kính là bao nhiêu, chỉ cần chia đôi nó ra bạn sẽ có được bán kính.

• Theo ví dụ trên, hình tròn với đường kính 20 cm sẽ có bán kính là 20/2 = 10 cm.

Áp dụng công thức dính diện tích cơ bản

Sau khi chuyển đổi đường kính thành bán kính, đây là lúc bạn sử dụng công thức {displaystyle A=pi r^{2}} để tính diện tích hình tròn. Gán giá trị của bán kính vào và tiến hành phép tính còn lại như sau:

• 
• 
• 

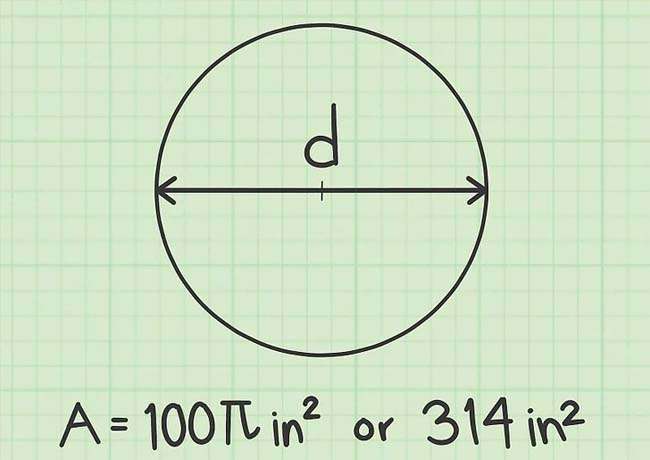
Trình bày giá trị của diện tích

Xin nhắc lại, đơn vị diện tích của hình tròn sẽ đi cùng với dấu “bình phương”. Trong ví dụ này, đường kính được tính bằng cm, vì thế, bán kính cũng được tính bằng cm. Vậy, diện tích sẽ được tính theo cm vuông. Đáp số ở đây sẽ là  cm².

• Bạn cũng có thể cung cấp một số thập phân bằng cách thay 3,14 cho . Kết quả của biểu thức là (100)(3,14) = 314 cm².

Công thức tính dựa vào chu vi hình tròn

S = C²/(4Pi)

Trong đó: C là chu vi

Chứng minh công thức:
Ta có: Chu vi hình tròn C = 2Pi.r
=> r = C/(2Pi)
=> Diện tích hình tròn là: S =C²/(4Pi)

Ví dụ: Cho hình trong C có chi vi là 16cm2. Tính diện tích hình tròn C.

Giải: Ta có chu vi hình tròn C = 2Pi.r => r = C/(2Pi)
Do đó, diện tích hình tròn là S = C²/(4Pi) = 20,382cm2

Công thức tính dựa vào hình quạt

Trong đó, S: Diện tích toàn phần hình tròn
Shq: Diện tích hình quạt
C: Số đo góc ở tâm

Công Thức Tính Diện Tích Hình Quạt Tròn

Trong hình tròn bán kính R diện tích hình tròn n được tính theo công thức là:

Trong đó,

– n là góc của hình quạt tròn
– l là độ dài cung n trong hình quạt

Phương Pháp Nhớ Công Thức, Cách Tính Diện Tích Hình Tròn

Các kiến thức, công thức tính toán liên quan đến hình học đều rất quan trọng với các em học sinh bởi các dạng bài tập liên quan đến hình tròn khá phổ biến trong chương trình học, các em cần nắm vững những kiến thức này. Công thức tính chu vi hình tròn, diện tích hình tròn hay công thức tính diện tích tam giác, diện tích hình thang là các kiến thức nền tảng và vô cùng quan trọng giúp các em học sinh, sinh viên hoặc những ngưởi có công việc liên quan đến tính toán và đo đạc như kỹ sư, thiết kế.

CÁCH TÍNH CHU VI HÌNH TRÒN VÀ DIỆN TÍCH HÌNH TRÒN

1. Hình Tròn Là Gì?

Trên một mặt phẳng, hình tròn là vùng trên mặt phẳng nằm “trong” đường tròn. Chu vi, bán kính và tâm của hình tròn là tâm và bán kính của đường tròn bao quanh nó. Tùy vào việc nó chứa hoặc không chứa đường tròn biên mà hình tròn đó gọi là đóng hoặc mở. 

2. Chu Vi Hình Tròn

– Khái niệm về chu vi hình tròn: Chu vi hình tròn hay đường tròn là đường biên giới hạn của hình tròn. Công thức của chu vi hình tròn là lấy đường kính nhân với pi hay 2 lần bán kính nhân pi.

– Công thức tính chu vi hình tròn:C=d x Pi hoặc C = (r x 2) x Pi
Trong đó:
C: chu vi hình tròn
d: đường kính hình tròn
Pi : Số Pi (~3,141…)
r: bán kính hình tròn

– Ví dụ : Có một hình tròn C có đường kính nối từ điểm AB = 10cm. Hỏi chu vi hình tròn C bằng bao nhiêu?
Ta áp dụng: cách tính chu vi hình tròn đã có ở trên: d = AB = 10 cm. Như vậy:
C = d x Pi = 10 x Pi = 10 x 3,14 = 31,4 cm

3. Diện Tích Hình Tròn

– Khái niệm diện tích hình tròn: Diện tích hình tròn được tính bằng độ lớn của hình tròn chiếm trên một bề mặt nhất định.
* Công thức tính diện tích hình tròn: S = Pi x r²

Trong đó:
r : Bán kính hình tròn và bằng 1/2 đường kính (d)
Pi: Số Pi (~3,141…)

– Ví dụ: Ta có một hình tròn C có đường kính d=10cm. Hỏi diện tích hình tròn C bằng bao nhiêu?
Áp dụng cách tính: diện tích hình tròn C ta có: r = 1/2 x d = 1/2×10 = 5cm
Suy ra: S = Pi x r² = 5 x (3,14)² = 49,298 cm2

* Công thức tính diện tích đường tròn khi biết đường kính: S = Pi X (D/2)²

– Trong đó: d là đường kính

– Ví dụ: Ta có hình tròn C với đường kính là 8cm. Tính diện tích hình tròn C.
Áp dụng cách tính, S = Pi x (d/2)^2 = 50,265cm2

* Công thức tính dựa vào chu vi hình tròn: S = C²/(4Pi) 

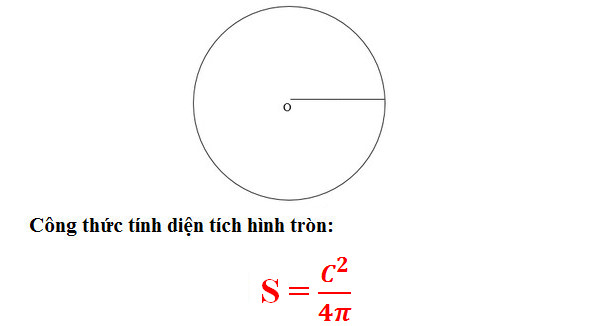
Trong đó: C là chu vi

Chứng minh công thức:
Ta có: Chu vi hình tròn C = 2Pi.r
=> r = C/(2Pi)
=> Diện tích hình tròn là: S =C²/(4Pi)

Ví dụ: Cho hình trong C có chi vi là 16cm2. Tính diện tích hình tròn C.

Giải: Ta có chu vi hình tròn C = 2Pi.r => r = C/(2Pi)
Do đó, diện tích hình tròn là S = C²/(4Pi) = 20,382cm2

* Công thức tính dựa vào hình quạt: 

Trong đó, S: Diện tích toàn phần hình tròn
Shq: Diện tích hình quạt
C: Số đo góc ở tâm

4. Công Thức Tính Diện Tích Hình Quạt Tròn

Trong hình tròn bán kính R diện tích hình tròn n được tính theo công thức là:

Trong đó,

– n là góc của hình quạt tròn
– l là độ dài cung n trong hình quạt

5. Phương Pháp Nhớ Công Thức, Cách Tính Diện Tích, Chu Vi Hình Tròn

– Khi học công thức xong cũng như cách tính, bạn nên vận dụng vào làm bài tập để có thể ghi nhớ công thức cũng như hiểu được rõ bản chất vấn đề. 
– Bên cạnh đó, bạn có thể học công thức thông qua thơ:

Hình tròn diện tích đơn giản
Bình phương bán kính ta nhân ngay vào
Ba phảy mười bốn phía sau

Bài tập về cách tính diện tích hình tròn

Một ví dụ thực tế

Max đang xây một ngôi nhà. Trước hết, anh ấy cần khoan lỗ và lấp đầy bê tông vào chúng. Các lỗ này có chiều rộng 0.4m, độ sâu 1m.Hỏi Max cần đổ bao nhiêu bê tông vào mỗi lỗ?

Cách giải như sau:

Các lỗ có hình tròn (ở mặt cắt ngang) bởi chúng được đục bằng máy khoan.

Với đường kính 0.4m, diện tích của hình là:

A = (π/4) × D2

A = (3.14159…/4) × 0.42

A = 0.7854… × 0.16

A = 0.126m²

Lỗ có độ sâu 1m nên thể tích của nó là:

Thể tích = 0.126m² × 1 m = 0.126m³

Kết luận, Max cần đổ 0.126m³ bê tông vào mỗi lỗ.

Tính diện tích hình tròn, khi biết chu vi c bằng 15,33cm

Bài giải:

– Ta có, chu vi hình tròn  C = d.Pi = 2r.Pi => r = C/(2Pi)
– Diện tích hình tròn là S = Pi.r²
=> S = Pi. (C/2Pi)²  =   18,71cm2
Vậy diện tích hình tròn là 18,71cm2

Bài toán: tính diện tích hình tròn ở trên khi biết r = 4 cm.

– Bài giải: Áp dụng công thức ở trên chúng ta sẽ có

Vậy diện tích của hình tròn trên là 50,24 cm2

Tính s hình tròn từ đường kính d

Bài 1: Cho hình tròn C có đường kính d = 16 cm. Hãy tính S(diện tích) hình tròn C?

Giải: Ta có, bán kính bằng một nữa đường kính theo công thức: R = d/2

R = 16/2 = 8 cm

S hình tròn C: S = πR² = 3,14.8² = 200,96 cm²

Tính diện tích hình vành khăn

Bài 2: Tính diện tích phần tô màu xám trong hình vẽ bên dưới đây. Biết, đường tròn lớn bao quanh bên ngoài có bán kính r₂ = 15 cm và đường tròn nhỏ bên trong có bán kính r₁ = 10 cm.

Giải: Nhận xét: Từ hình vẽ ta thấy, diện tích phần tô màu xám trong hình bằng hiệu của S hình tròn lớn bán kính r₂ và DT(diện tích) hình tròn nhỏ bán kính r₁.

– S hình tròn nhỏ:

S₁ = πr₁² = 3,14.10² = 314 cm²

– DT hình tròn lớn:

S₂ = πr₂² = 3,14.15² = 706,5 cm²

– Diện tích hình màu xám trong hình:

S = S₂ – S₁ = 706,5 – 314 = 392,5 cm²

Tính diện tích hình bất kỳ có chứa 1 phần diện tích hình tròn

Bài 3: Tính diện tích toàn bộ hình vẽ bên dưới?

Giải: Ta thấy, diện tích của hình trên bao gồm diện tích 2 nữa hình tròn bán kính r =7 cm và diện tích của hình chữ nhật kích thước 10×7 cm.

– Diện tích hình chữ nhật: S₁ = 10 x 7 = 70 cm²

– Diện tích hai nữa hình tròn cùng bán kính: S₂ = πR² = 3,14.7² = 153,86 cm²

=> Diện tích hình đã cho: S = S₂ + S₁ = 70 + 153,86 = 223,86 cm²

Bài toán tính S từ d nâng cao

Bài 4: Tính S hình tròn, biết nếu tăng đường kính đường tròn lên 30% thì DT hình tròn tăng thêm 20 cm²

Giải: Nếu tăng đường kính của hình tròn lên 30% thì bán kính cũng tăng 30%

Số % S(diện tích) được tăng thêm là:

(130%)² – (100%)² = 69%

Vậy diện tích hình tròn ban đầu là: 20×100/69 = 29,956 cm²