Tam giác cân Là tài liệu vô cùng hữu ích mà THPT Phạm Hồng Thái mong muốn giới thiệu tới quý thầy cô giáo và các em học sinh lớp 7 làm tài liệu tham khảo.
Tam giác cân là tam giác có hai cạnh bằng nhau. Đỉnh của tam giác cân là giao điểm của hai cạnh. Góc tạo bởi đỉnh gọi là góc đỉnh, hai góc còn lại gọi là góc đáy. Vậy công thức tính diện tích tam giác cân là gì? Tính chất của tam giác cân là gì? Làm thế nào để chứng minh một tam giác cân? Mời các bạn cùng theo dõi trong bài viết dưới đây.
1. Định nghĩa tam giác cân
Tam giác cân Là tam giác có hai cạnh bằng nhau, hai cạnh này gọi là cạnh bên. Đỉnh của tam giác cân là giao điểm của hai cạnh. Góc tạo bởi đỉnh gọi là góc đỉnh, hai góc còn lại gọi là góc đáy.
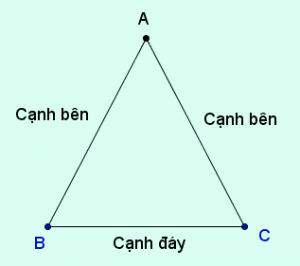
Trong hình trên, tam giác ABC có AB = AC nên tam giác ABC cân.
Vì AB và AC là hai cạnh nên tam giác ABC cân ở đỉnh A.
2. Tính chất của tam giác cân
Một tam giác cân có bốn tính chất sau:
Nguồn 1: Trong một tam giác cân, hai góc ở đáy bằng nhau.
Để kiểm tra:
| Giả thuyết | Tam giác ABC cân tại A, AB = AC |
| Hoàn thiện |
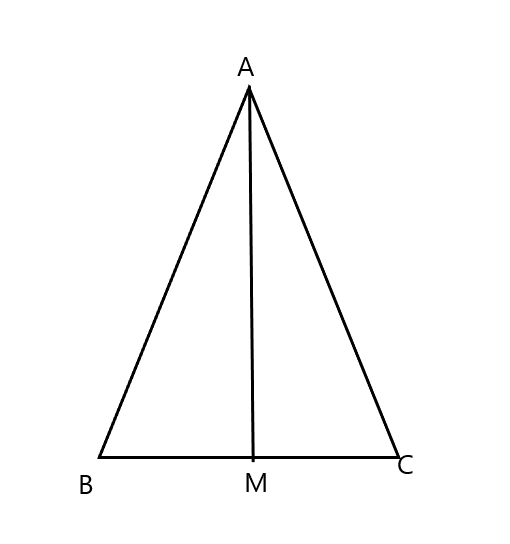
Trong tam giác cân ABC, gọi AM là tia phân giác của góc.
Vì vậy chúng tôi có
Xét tam giác ABM và tam giác ACM là:
AB = AC (gt)
(centimet)
AM chung
Ta coi ABM = ΔACM (cgc). (dpcm)
Nguồn 2: Tam giác có hai góc bằng nhau là tam giác cân.
để kiểm tra
| Giả thuyết | tam giác ABC, |
| Hoàn thiện | Tam giác ABC cân tại điểm A |
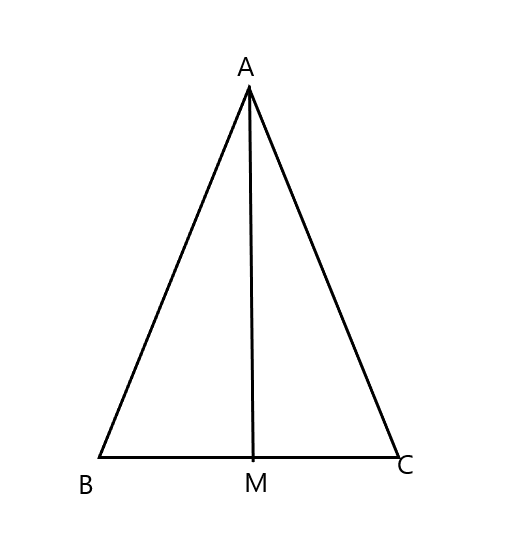
Trong tam giác ABC, AM là tia phân giác.
tam giác ABM (tổng 3 góc trong một tam giác)
Tam giác ACM (tổng 3 góc trong một tam giác)
Nhưng có
chân đèn
Xét tam giác ABM và tam giác ACM là:
ΔABM = ΔACM (g – g – g) thì AB = AC (các cạnh tương ứng bằng nhau)
Xét tam giác ABC có AB = AC, kết luận tam giác ABC cân tại điểm A (định nghĩa)
Nguồn 3: Trong một tam giác cân, đường trung trực là đường phân giác, đường trung bình và đường cao của tam giác.
Nguồn 4: Nếu một tam giác có đường trung tuyến cũng là đường phân giác thì tam giác đó là tam giác cân.
3. Dấu hiệu xác định tam giác cân
Một tam giác cân có hai dấu hiệu:
- Kí hiệu 1: Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.
- Kí hiệu 2: Nếu hai góc của một tam giác đồng dạng thì tam giác đó là cân.
4. Diện tích tam giác cân
Diện tích tam giác đều Tích của chiều cao nối đỉnh của tam giác với đáy của tam giác rồi chia cho 2.
Công thức tính diện tích tam giác cân: S = (axh) / 2
Ở đó:
- a: Độ dài cạnh đáy của tam giác cân (đáy là một trong ba cạnh của tam giác)
- h: Chiều cao của hình tam giác (chiều cao của hình tam giác bằng một phần của nó từ trên xuống dưới).
5. Cách chứng minh tam giác cân
– Cách 1: Chứng minh một tam giác có hai cạnh bằng nhau.
– Cách 2: Chứng minh tam giác có hai góc bằng nhau.
Ví dụ 1: Tam giác ABC có Δ ABD = Δ ACD. Chứng minh rằng tam giác ABC cân.

+ Chứng minh Dạng 1:
Theo kết quả đầu ra, chúng ta có:
Δ Mỹ = ACD
=> AB = AC
=> Tam giác ABC cân tại điểm A
+ Chứng minh Dạng 2:
Theo kết quả đầu ra, chúng ta có:
∆ Mỹ = ACD
=> Góc B = C
=> Tam giác ABC cân tại điểm A
Ví dụ 2:
Cho ABC là tam giác cân tại điểm A. Lấy điểm D trên cạnh AC và điểm E trên cạnh AB sao cho AD = AE.
a) So sánh các góc ABD và ACE
b) Gọi giao điểm của BD và CE là I. ΔIBC là tam giác gì? Tại sao ?
Câu trả lời được đề xuất
a) Tam giác ABC cân tại điểm A (phỏng đoán)
Xét ΔABD và ΔACE:
AB = AC (giả thiết)
đã chia sẻ
AD = AE (giả định)
⇒ ΔABD = ACE (cạnh – góc – cạnh)
(cặp góc phù hợp)
b) ΔIBC chứa:
ΔIBC là tôi có trọng số
6. Bài tập tam giác cân
bài kiểm tra
Bài 1: Chọn biểu thức sai
A. Một tam giác đều có ba góc bằng nhau và bằng 60 °
B. Một tam giác đều có ba cạnh bằng nhau.
C. Tam giác cân là tam giác đều.
D. Tam giác đều là tam giác cân.
Đề nghị
Bài 2: Hai góc nhọn của tam giác vuông cân
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Bài 3: Cho ABC là tam giác cân tại điểm A. Chọn biểu thức sai
Đề nghị
Bài 4: Nếu góc ở đỉnh của tam giác cân bằng 64 ° thì số đo của góc ở đáy là bao nhiêu?
A. 54 °
B. 58 °
độ 72 °
D. 90 °
Đề nghị
Bài 5: Nếu góc ở đáy của tam giác cân là 70 ° thì góc của khối chóp là bao nhiêu?
A. 64 °
B. 53 °
C. 70 °
D. 40 °
B. Kiểm tra
Bài 1. Mỗi ABC A cân bằng trên có
. Tìm số đo của các góc B và C.
Bài 2. Mỗi ABC A cân bằng trên có
. Tìm số đo của các góc B và C.
Bài 3. Mỗi Trọng lượng tính bằng P
. Tính số đo các góc
Bài thứ 4. Mỗi ABC là hình vuông cân bằng A. Tìm số đo các góc B và C.
Bài 5. Mỗi ABC A cân bằng trên có
Tìm số đo của góc A và C.
6. Bài học. Mỗi vảy tai
. Tìm số đo các góc M và F
7. Bài học. Mỗi Quy mô tai Q có
. Tìm số đo các góc P và Q
Bài 8. Mỗi ABC là góc vuông cân ở A. Trên tia đối của tia BC lấy điểm D sao cho BD = AB B. Tính số đo của góc ADB.
9. Bài học Mỗi trọng lượng A có
. Hai tia phân giác của góc B và C cắt nhau tại I. Tìm số đo của góc BIC.
Bài 10. Mỗi ABC cân bằng A. Hai đường phân giác của góc B và C cắt nhau tại tai I có số đo đã biết.
. Tính số đo của góc A.
11. Bài học. cho tam giác ABC cân đối trên A có
. Tia phân giác của góc B cắt tai AC I. Tính số đo của góc BIC
bài 12: Cho góc hẹp là xOy. Điểm H nằm trên tia phân giác của góc xOy. Từ H kẻ các đường vuông góc xuống hai cạnh Ox và Oy (A thuộc Ox và B thuộc Oy).
a) Chứng minh rằng tam giác HAB là tam giác cân
b) D là hình chiếu của điểm A trên Oy, C là giao điểm của AD và O. Chứng minh BC ⊥ Ox.
c) Khi góc xOy bằng 600chứng minh OA = 2O
Bài 13: ∆Cho ABC cân tại điểm A và trung tuyến BM, CN cắt nhau tại điểm K.
a) Chứng minh rBNC = rCMB
b) Chứng minh rằng BKC nằm trong K
c) Chứng minh BC
14. Bài học: ∆ Cho ABC vuông trên A với BD là tia phân giác, vẽ DE ⊥ BC (E∈BC). Gọi giao điểm của AB và DE là F. chứng minh điều đó
a) BD là tia phân giác của AE
b) DF = DC
c) AD
- #Tam #giác #cân #Khái #niệm #tính #chất #cách #chứng #minh #và #bài #tập




