Hỗn số là gì? Cách tính hỗn số và bài tập ví dụ minh họa có đáp án

Hỗn số là gì? Cách tính hỗn số và bài tập ví dụ minh họa có đáp án. Hỗn số là một trường hợp đặc biệt của phân số trong toán học, nó giúp biểu diễn các tỉ lệ mà phân số không thể hiện được. Đây là khái niệm được giảng dạy trong chương trình toán học lớp 5. Thầy cô trường Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội mời các em theo dõi bài học hôm nay nhé.

Nội dung chính

Định nghĩa hỗn số là gì?

Hỗn số là kết quả của việc viết gọn tổng của một số tự nhiên nguyên dương với một phân số dương bằng cách bỏ dấu cộng xen giữa chúng. Như vậy, một hỗn số gồm hai phần: phần nguyên và phần phân số.
Số đối của hỗn số này cũng được gọi là một hỗn số.
Hỗn số được viết dưới dạng $afrac{b}{c}$ . Phần phân số của hỗn số luôn luôn nhỏ hơn 1.

$a+frac{b}{c}=afrac{b}{c}$

Ví dụ:

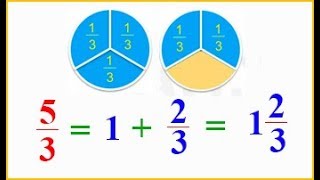
Cách đổi hỗn số thành phân số

$afrac{b}{c}$

Đổi phân số hoặc hỗn số dương

Nếu phân số dương lớn hơn 1, ta có thể viết nó dưới dạng hỗn số bằng cách: chia tử cho mẫu. Thương tìm được là phần nguyên của hỗn số, phần phân số có tử là số dư là tử, còn mẫu vẫn là mẫu đã cho.
Nếu muốn đổi một hỗn số dương dưới dạng một phân số, thực hiện nhân phần số nguyên với mẫu rồi cộng với tử, kết quả tìm được là tử của phân số, còn mẫu vẫn là mẫu đã cho.

Đổi phân số hoặc hỗn số âm

Khi viết một phân số âm dưới dạng hỗn số, ta chỉ cần viết số đối của nó dưới dạng hỗn số rồi đặt dấu trước kết quả nhận được.
Tương tự như vậy, khi viết một hỗn số âm dưới dạng phân số, chỉ cần viết số đối của nó dưới dạng phân số rồi đặt dấu “-“ trước kết quả.

Các dạng toán về hỗn số lớp 5

Cách cộng hỗn số

Phương pháp giải:

Khi cộng hai hỗn số: có thể viết chúng dưới dạng phân số rồi thực hiện phép cộng phân số. Ta cũng có thể cộng phần nguyên với nhau, cộng phần phân số với nhau (khi hai hỗn số đều dương).

Ví dụ:

$2frac{1}{2}+3frac{1}{4}=(2+3)+(frac{1}{2}+frac{1}{4})=5+frac{3}{4}=5frac{3}{4}$

Cách trừ hỗn số

Phương pháp giải:

Khi trừ hai hỗn số: có thể viết chúng dưới dạng phân số rồi thực hiện phép trừ phân số. Ta cũng có thể lấy phần nguyên của số bị trừ trừ phần nguyên của số trừ, phần phân số của số bị trừ trừ phần phân số của số trừ, rồi cộng hai kết quả với nhau (khi hai hỗn số đều dương, số bị trừ lớn hơn hoặc bằng số trừ).
Khi hai hỗn số đều dương, số bị trừ lớn hơn hoặc bằng số trừ, nhưng phần phân số của số bị trừ nhỏ hơn phần phân số của số trừ, phải thực rút một đơn vị ở phần nguyên của số bị trừ để thêm vào phần phân số, sau đó tiếp tục trừ như trên.

Cách nhân chia hỗn số

Phương pháp giải:

Khi nhân hoặc chia một hỗn số với một số nguyên, có thể viết hỗn số dưới dạng tổng của một số nguyên và một phân số.

Tính giá trị của biểu thức

Phương pháp giải:

Để có thể tính giá trị của các biểu thức số cần chú ý:

Thứ tự thực hiện các phép tính.
Căn cứ vào đặc điểm của các biểu thức ta có thể áp dụng tính chất các phép tính và quy tắc dấu ngoặc.

Viết phân số dưới dạng hỗn số

Phương pháp giải:

Áp dụng quy tắc viết phân số dưới dạng hỗn số và quy tắc viết hỗn số dưới dạng phân số.

Ví dụ: Viết các phân số sau dưới dạng hỗn số :

$frac{7}{3};frac{-15}{11}$

Cách giải:

$frac{7}{3}=2frac{1}{3}$

$frac{-15}{11}=-1frac{4}{11}$

Ví dụ: Viết các hỗn số sau dưới dạng phân số :

$3frac{2}{8};-2frac{5}{13}$

Cách giải:

$3frac{2}{8}=frac{26}{8}$

$-2frac{5}{13}=-frac{31}{13}$

Cách tính nhanh hỗn số

Khi thực hiện cộng hai hỗn số $2frac{2}{3}; 3frac{1}{5}$ , ta có thể tính nhanh hơn bằng cách cộng phần nguyên với phần nguyên, phần phân số với phần phân số rồi cộng hai kết quả lại với nhau.

$2frac{2}{3}+3frac{1}{5}=(3+2)+(frac{2}{3}+frac{1}{5})=5+frac{13}{15}=5frac{13}{15}$

Mối liên hệ giữa phân số và hỗn số

– Chuyển hỗn số thành phân số

Phân số được chuyển từ hỗn số có:
Mẫu số bằng với mẫu số của phân số.
Tử số bằng với mẫu số nhân phần nguyên cộng Tử số của phần phân số.

– Chuyển phân số thành hỗn số

Khi phân số lớn hơn 1 (tử số lớn hơn mẫu số).
Có thể thực hiện chuyển phân số đó về dạng hỗn số.

Bài tập về Hỗn số lớp 5

Toán lớp 5 trang 12, 13 tập 1

Giải Toán lớp 5 trang 12 bài 1

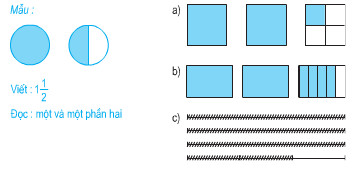
Dựa vào hình vẽ để viết rồi đọc hỗn số thích hợp (theo mẫu):

Hướng dẫn:

– Quan sát hình vẽ để viết hỗn số thích hợp với mỗi hình.

– Khi đọc (hoặc viết) hỗn số ta đọc (hoặc viết) phần nguyên rồi đọc (hoặc viết) phần phân số.

Đáp án:

a) $2frac{1}{4}$ : Hai và một phần tư.

b) $2frac{4}{5}$ : Hai và bốn phần năm.

c) $3frac{2}{3}$ : Ba và hai phần ba.

Giải Toán lớp 5 trang 13 bài 2

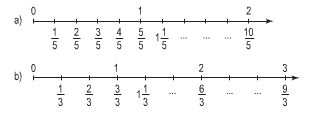
Viết hỗn số thích hợp vào chỗ chấm dưới mỗi vạch của tia số:

Hướng dẫn:

– Quan sát hình vẽ để viết hỗn số thích hợp với mỗi hình.

– Khi viết hỗn số ta viết phần nguyên rồi viết phần phân số.

Đáp án:

Điền từ trái qua phải:

a) $1 frac{2}{5} ; 1 frac{3}{5} ; 1 frac{4}{5}$

b) $1 frac{2}{3} ; 2 frac{1}{3} ; 2 frac{2}{3}$

Toán lớp 5 trang 13, 14 tập 1

Giải Toán lớp 5 trang 13 bài 1

Chuyển các hỗn số sau thành phân số:

$displaystyle 2{1 over 3};quad 4{2 over 5};quad3{1 over 4};quad9{5 over 7};quad10{3 over {10}}$

Hướng dẫn:

Có thể viết hỗn số thành một phân số có:

– Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

– Mẫu số bằng mẫu số ở phần phân số.

Đáp án:

$displaystyle2{1 over 3} = { 2 times 3 + 1 over 3}= {7 over 3} ;$

$displaystyle4{2 over 5} = { 4 times 5 + 2 over 5}= {{22} over 5} ;$

$displaystyle3{1 over 4} = { 3 times 4 + 1 over 4} ={{13} over 4} ;$

$displaystyle9{5 over 7} = { 9 times 7 + 5 over 3}= {{68} over 7} ;$

$displaystyle10{3 over {10}} = {10 times 10 + 3 over {10} }={{103} over {10}}.$

Giải Toán lớp 5 trang 14 bài 2

Chuyển các hỗn số sau thành phân số rồi thực hiện phép tính (theo mẫu):

$a) 2dfrac{1}{3}+4dfrac{1}{3} ;$

$b) 9dfrac{2}{7}+5dfrac{3}{7}$

$c) 10dfrac{3}{10}-4dfrac{7}{10}$

Mẫu:

$a) 2dfrac{1}{3}+4dfrac{1}{3} =dfrac{7}{3}+dfrac{13}{3}=dfrac{20}{3}$

Hướng dẫn:

Chuyển các hỗn số thành phân số rồi thực hiện phép cộng hoặc phép trừ phân số như thông thường.

Đáp án:

b) Ta có :

$eqalign{ & 9{2 over 7} = {{9 times 7 + 2} over 7} = {{65} over 7} cr & 5{3 over 7} = {{5 times 7 + 3} over 7} = {{38} over 7} cr}$

$9dfrac{2}{7}+5dfrac{3}{7}=dfrac{65}{7}+dfrac{38}{7}=dfrac{103}{7}$

c) Ta có:

$eqalign{ & 10{3 over {10}} = {{10 times 10 + 3} over {10}} = {{103} over {10}} cr & 4{7 over {10}} = {{4 times 10 + 7} over {10}} = {{47} over {10}} cr}$

$10dfrac{3}{10}-4dfrac{7}{10}=dfrac{103}{10}-dfrac{47}{10}=dfrac{56}{10}=dfrac{28}{5}$

Giải Toán lớp 5 trang 14 bài 3

Chuyển các hỗn số sau thành phân số rồi thực hiện phép tính (theo mẫu):

$eqalign{ & a),,2{1 over 3} times 5{1 over 4}, cr & b),,3{2 over 5} times 2{1 over 7} & ,,,,,,,,,,, cr & c),8,{1 over 6}:2{1 over 2} cr}$

Mẫu:

$a)2dfrac{1}{3} times 5dfrac{1}{4} = dfrac{7}{3} times dfrac{{21}}{4} = dfrac{{49}}{4}$

Hướng dẫn:

Chuyển các hỗn số thành phân số rồi thực hiện phép nhân, phép chia phân số như thông thường.

Đáp án:

$b) displaystyle 3{2 over 5} times 2{1 over 7} = {{17} over 5} times {{15} over 7} = dfrac{17times 15}{5 times 7} displaystyle = dfrac{17times 5 times 3}{5 times 7}={{51} over 7}$

$c) displaystyle 8{1 over 6}:2{1 over 2} = {{49} over 6}:{5 over 2}= {{49} over 6} times {2 over 5} displaystyle = dfrac{49times 2 }{3 times 2 times 5}={{49} over {15}}$

Giải Vở bài tập Toán lớp 5 tập 1 trang 11

Vở bài tập Toán lớp 5 tập 1 trang 11 Câu 1

Viết (theo mẫu)

$displaystyle displaystyle 1{1 over 4}$

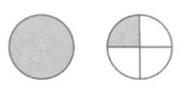
Đọc: Một và một phần tư

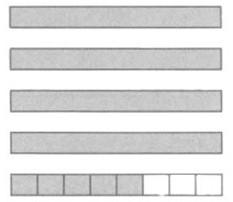
Hướng dẫn giải

– Quan sát hình vẽ để viết hỗn số thích hợp với mỗi hình.

– Khi đọc (hoặc viết) hỗn số ta đọc (hoặc viết) phần nguyên rồi đọc (hoặc viết) phần phân số.

Đáp án chi tiết

a) Viết: $displaystyle 1{1 over 4}$ ; Đọc: Một và một phần tư.

b) Viết: $displaystyle 3{1 over 6}$ ; Đọc: Ba và một phần sáu.

c) Viết: $displaystyle 2{3 over 4}$ ; Đọc: Hai và ba phần tư.

d) Viết: $displaystyle 4{5 over 8}$ ; Đọc: Bốn và năm phần tám.

Vở bài tập Toán lớp 5 tập 1 trang 12 Câu 2

Viết hỗn số thích hợp vào chỗ chấm dưới mỗi vạch của tia số

Hướng dẫn giải:

– Quan sát hình vẽ để viết hỗn số thích hợp với mỗi vạch của tia số.

– Khi viết hỗn số ta viết phần nguyên rồi viết phần phân số.

– Viết các hỗn số theo thứ tự tăng dần của trục số

Đáp án chi tiết

Vở bài tập Toán lớp 5 tập 1 trang 12 Câu 3

Viết tiếp vào chỗ chấm cho thích hợp

Giải thích vì sao: $displaystyle 3{1 over 4} = {{13} over 4};?$

Ta có: $displaystyle 3{1 over 4} = 3 + {1 over 4} = ..................$

Hướng dẫn giải:

Viết 3 dưới dạng phân số có mẫu số là 1, sau đó thực hiện phép cộng hai phân số như thường.

Lời giải chi tiết:

Ta có:

$displaystyle 3{1 over 4} = 3 + {1 over 4} = {{12} over { 4}} + {1 over 4} = {{12 + 1} over 4} displaystyle = {{13} over 4}.$

Vở bài tập Toán lớp 5 tập 1 trang 12 Câu 1

Chuyển hỗn số thành phân số (theo mẫu)

Mẫu: $displaystyle 5{1 over 2} = {{5 times 2 + 1} over 2} = {{11} over 2}$

a) $displaystyle 3{1 over 5} =; ...................$

b) $displaystyle 8{4 over 7} = ;...................$

c) $displaystyle 12{5 over {12}} =; .................$

Hướng dẫn:

Có thể viết hỗn số thành một phân số có:

– Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

– Mẫu số bằng mẫu số ở phần phân số.

Đáp án:

a) $displaystyle 3{1 over 5} = {{3 times 5 + 1} over 5} = {{16} over 5}$

b) $displaystyle 8{4 over 7} = {{8 times 7 + 4} over 7} = {{56 + 4} over 7} = {{60} over 7}$

c) $displaystyle 12{5 over {12}} = {{12 times 12 + 5} over {12}} = {{144 + 5} over {12}} displaystyle = {{149} over {12}}$

Vở bài tập Toán lớp 5 tập 1 trang 12 Câu 2

Chuyển các hỗn số thành phân số rồi thực hiện phép tính (theo mẫu)

Mẫu: $displaystyle 2{1 over 4} + 1{1 over 7} = {9 over 4} + {8 over 7} = {{63} over {28}} + {{32} over {28}} displaystyle= {{95} over {28}}$

a) $displaystyle 3{1 over 2} + 2{1 over 5} = ;...............$

b) $displaystyle 8{1 over 3} - 5{1 over 2} = ;...............$

c) $displaystyle 6{1 over 7} times 1{6 over {43}} =;..............$

d) $displaystyle 9{1 over 5}:4{3 over 5} = ;................$

Hướng dẫn:

Chuyển các hỗn số thành phân số rồi thực hiện phép cộng hoặc phép trừ phân số như thông thường.

Đáp án:

a) $displaystyle 3{1 over 2} + 2{1 over 5} = {7 over 2} + {{11} over 5} = {{35} over {10}} + {{22} over {10}} displaystyle = {{57} over {10}} = 5{7 over {10}}$

b) $displaystyle 8{1 over 3} - 5{1 over 2} = {{25} over 3} - {{11} over 2} = {{50} over 6} - {{33} over 6} displaystyle= {{17} over 6} = 2{5 over 6}$

c) $displaystyle 6{1 over 7} times 1{6 over {43}} = {{43} over 7} times {{49} over {43}} = {{43 times 49} over {7 times 43}} displaystyle= {{49} over 7} = 7$

d) $displaystyle 9{1 over 5}:4{3 over 5} = {{46} over 5}:{{23} over 5} = {{46} over 5} times {5 over {23}} displaystyle= {{46 times 5} over {5times 23}}= {{23 times 2 times 5} over {5times 23}} =2$

Vở bài tập Toán lớp 5 tập 1 trang 13 Câu 3

Chuyển các hỗn số thành phân số rồi thực hiện phép tính

a) $displaystyle 2{1 over 5} times 3{4 over 9} = .....................$

b) $displaystyle 7{2 over 3}:2{1 over 4} = ......................$

c) $displaystyle 4{2 over 3} + 2{3 over 4} times 7{3 over {11}} = ..............$

Hướng dẫn:

Chuyển các hỗn số thành phân số rồi thực hiện phép nhân, phép chia phân số như thông thường.
Biểu thức có phép cộng và phép nhân thì thực hiện phép nhân trước, thực hiện phép cộng sau.

Đáp án:

a) $displaystyle 2{1 over 5} times 3{4 over 9} = {{11} over 5} times {{31} over 9} = {{11 times 31} over {5 times 9}} displaystyle= {{341} over {45}}$

b) $displaystyle 7{2 over 3}:2{1 over 4} = {{23} over 3}:{9 over 4} = {{23} over 3}times {4 over 9} = displaystyle {{23 times 4} over {3 times 9}} = {{92} over {27}}$

c) $displaystyle 4{2 over 3} + 2{3 over 4} times 7{3 over {11}} = {{14} over 3} + {{11} over 4} times {{80} over {11}}$

$displaystyle = {{14} over 3} + dfrac{11 times 80}{4 times 11} ={{14} over 3} +dfrac{ 80}{4 }$

$displaystyle= {{14} over 3} +20 = {{14} over 3} + dfrac{ 60}{3 }=dfrac{74}{3}$

Học sinh có thể giải theo cách khác dưới đây:

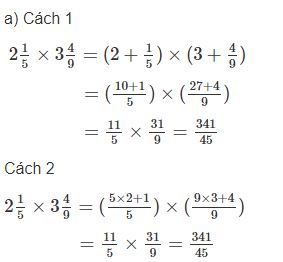
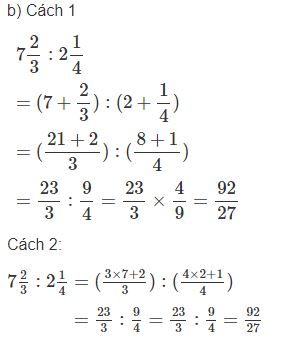
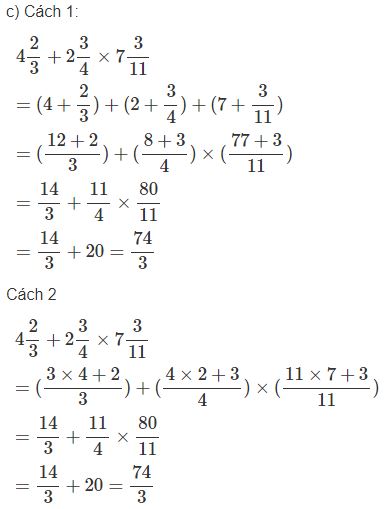
Giải Vở bài tập Toán lớp 5 tập 1 trang 13

Vở bài tập Toán lớp 5 tập 1 trang 13 Bài 1

Điền dấu thích hợp vào chỗ chấm: >; <; =

$eqalign{ & 5{1 over 7};...;2{6 over 7},,,,,,,,,,,,,,,,,,,,,,,,,,,,,quad 3{2 over 7};...;3{5 over 7} cr & 8{6 over {10}};...;8{3 over 5},,,,,,,,,,,,,,,,,,,,,,,,,,,quad 9{1 over 2};...;5{1 over 2} cr}$

Phương pháp giải

Đổi các hỗn số thành phân số rồi so sánh các phân số đó.

Đáp án và lời giải chi tiết

a) $5dfrac{1}{{7}} = dfrac{{36}}{{7}};;;;2dfrac{6}{{7}} = dfrac{{20}}{{7}}.$

Mà $dfrac{{36}}{{7}} > {rm{ }}dfrac{{20}}{{7}}$

Vậy : $5dfrac{1}{{7}} > {rm{ }}2dfrac{6}{{7}}.$

b) $3dfrac{2}{{7}} = dfrac{{23}}{{7}};;;;3dfrac{5}{{7}} = dfrac{{26}}{{7}}$ .

Mà $dfrac{{23}}{{7}} < dfrac{{26}}{{7}}$

Vậy: $3dfrac{2}{{7}} < {rm{ }}3dfrac{5}{{7}}.$

c) $8dfrac{6}{{10}} = dfrac{{86}}{{10}};;;;8dfrac{3}{{5}} = dfrac{{43}}{{5}}$ .

Mà $dfrac{{43}}{{5}} = dfrac{{43 times 2}}{{5 times 2}} =dfrac{{86}}{{10}}$

Vậy: $8dfrac{6}{{10}} = {rm{ }}6dfrac{3}{{5}}.$

d) $9dfrac{1}{{2}} = dfrac{{19}}{{2}} ;;;;5dfrac{1}{2} = dfrac{{11}}{2}$ .

Mà $dfrac{{19}}{2} > dfrac{{11}}{2}$

Vậy : $9dfrac{1}{{2}} > {rm{ }}5dfrac{1}{2}.$

Vở bài tập Toán lớp 5 tập 1 trang 13 Bài 2

Chuyển các hỗn số sau thành phân số rồi thực hiện phép tính

a) $displaystyle 2{1 over 8} + 1{3 over 4} = .....$

$displaystyle 3{2 over 7} + 1{3 over 7} = .....$

b) $displaystyle 5{1 over 3} - 2{5 over 6} =.....$

$displaystyle 4{7 over 9} - 1{5 over 9} = .....$

c) $displaystyle 2{4 over 5} times 3{1 over 8} = .....$

$displaystyle 1{1 over 5}:1{4 over 5} = .....$

Phương pháp giải

*) Chuyển các hỗn số thành phân số rồi thực hiện phép cộng, trừ, nhân, chia hai phân số như thông thường.

*) Cách chuyển hỗn số thành phân số :

Có thể viết hỗn số thành một phân số có:

– Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

– Mẫu số bằng mẫu số ở phần phân số.

Đáp án và hướng dẫn giải

+) $displaystyle 2{1 over 8} + 1{3 over 4} = {{17} over 8} + {7 over 4} = {{17} over 8} + {{14} over 8} displaystyle = {{31} over 8}$

+) $displaystyle 3{2 over 7} + 1{3 over 7} = {{23} over 7} + {{10} over 7} = {{33} over 7}$

+) $displaystyle 5{1 over 3} - 2{5 over 6} = {{16} over 3} - {{17} over 6} = {{32} over 6} - {{17} over 6} displaystyle = {{15} over 6} = {5 over 2}$

+) $displaystyle 4{7 over 9} - 1{5 over 9} = {{43} over 9} - {{14} over 9} = {{29} over 9}$

+) $displaystyle 2{4 over 5} times 3{1 over 8} = {{14} over 5} times {{25} over 8} = {{14 times 25} over {5 times 8}} displaystyle = {{350} over {40}} = {{35} over 4}$

+) $displaystyle 1{1 over 5}:1{4 over 5} = {6 over 5}:{9 over 5} = {6 over 5} times {5 over 9} dfrac{30}{45} = dfrac{2}{3}$

Vở bài tập Toán lớp 5 tập 1 trang 14 Bài 3

Tính

$displaystyle {{9 times 42} over {14 times 27}} =; ...............$

Phương pháp giải

Phân tích tử số và mẫu số thành tích của các thừa số, sau đó lần lượt chia tử số và mẫu số cho các thừa số chung.

Đáp án và hướng dẫn giải

$displaystyle {{9 times 42} over {14 times 27}} = {{not 9 times not3 times not14} over {not14 times not3 times not9}} = 1$

Khái niệm Hỗn số là gì là một khái niệm rất quen thuộc trong Toán học. Cách tính hỗn số cũng được chia thành các trường hợp khác nhau. Hy vọng thông qua bài viết này, thầy cô đã giúp các em hiểu rõ hơn về hỗn số cũng như biết cách tính để giải những bài Toán liên quan tới hỗn số.

Bản quyền bài viết thuộc trường Trường THPT Phạm Hồng Thái. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường THPT Phạm Hồng Thái (thpt-phamhongthai.edu.vn)